filmov
tv
How to expand a logarithmic expression with multiple logarithms

Показать описание
👉 Learn how to expand logarithmic expressions involving radicals. A logarithmic expression is an expression having logarithms in it. To expand logarithmic expressions means to use the logarithm laws to expand (open up) logarithm expressions from the condensed form to an expanded form. Knowledge of the logarithm laws/properties will be of importance in expanding logarithm expressions.
Some of the logarithm laws includes: the product law which states that the sum of individual logarithms of the same base is equivalent to the logarithm of the product of the terms in the individual logarithms. The quotient rule states that the difference between two individual logarithms of the same base is equivalent to the logarithm of the quotient of the terms in the individual logarithms. The power rule states that the multiple of the logarithm of a number is equivalent to the logarithm of the number raised to a power equivalent to the coefficient of the original logarithm.
Recall that the nth root of an expression/number is equivalent to the expression/number raised to the power of 1/n. To expand the logarithm of radical expressions, we first transform the radical to exponent form, then we use the power rule to take the exponent to the coefficient, and then we can use any other applicable logarithm law properties to expand the given expression.
Organized Videos:
✅Condense and Expand Logarithms
✅Condense Logarithms with Brackets
✅Rules of Logarithms
✅Condense Logarithms | Easy
✅Power Rule of Logarithms
✅Condense Logarithms | Hard
✅Product Rule of Logarithms
✅Power to Product Rule of Logarithms
✅Power to Quotient Rule of Logarithms
✅Expand Natural Logarithms
✅Expand Logarithms With Radicals
✅Convert Exponential to Logarithmic Form
✅Convert Logarithmic to Exponential
✅Logarithmic and Exponential Form | Learn About
Connect with me:
#logarithmicfunctions #brianmclogan
Some of the logarithm laws includes: the product law which states that the sum of individual logarithms of the same base is equivalent to the logarithm of the product of the terms in the individual logarithms. The quotient rule states that the difference between two individual logarithms of the same base is equivalent to the logarithm of the quotient of the terms in the individual logarithms. The power rule states that the multiple of the logarithm of a number is equivalent to the logarithm of the number raised to a power equivalent to the coefficient of the original logarithm.
Recall that the nth root of an expression/number is equivalent to the expression/number raised to the power of 1/n. To expand the logarithm of radical expressions, we first transform the radical to exponent form, then we use the power rule to take the exponent to the coefficient, and then we can use any other applicable logarithm law properties to expand the given expression.
Organized Videos:
✅Condense and Expand Logarithms
✅Condense Logarithms with Brackets
✅Rules of Logarithms
✅Condense Logarithms | Easy
✅Power Rule of Logarithms
✅Condense Logarithms | Hard
✅Product Rule of Logarithms
✅Power to Product Rule of Logarithms
✅Power to Quotient Rule of Logarithms
✅Expand Natural Logarithms
✅Expand Logarithms With Radicals
✅Convert Exponential to Logarithmic Form
✅Convert Logarithmic to Exponential
✅Logarithmic and Exponential Form | Learn About
Connect with me:
#logarithmicfunctions #brianmclogan
 0:04:36
0:04:36
 0:03:22
0:03:22
 0:03:45
0:03:45
 0:02:34
0:02:34
 0:03:28
0:03:28
 0:03:28
0:03:28
 0:00:48
0:00:48
 0:03:55
0:03:55
 0:02:10
0:02:10
 0:02:37
0:02:37
 0:03:41
0:03:41
 0:02:47
0:02:47
 0:01:33
0:01:33
 0:01:00
0:01:00
 0:00:44
0:00:44
 0:01:05
0:01:05
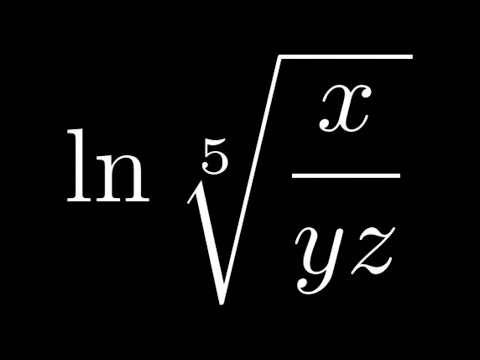 0:01:56
0:01:56
 0:02:42
0:02:42
 0:03:10
0:03:10
 0:01:54
0:01:54
 0:03:15
0:03:15
 0:02:22
0:02:22
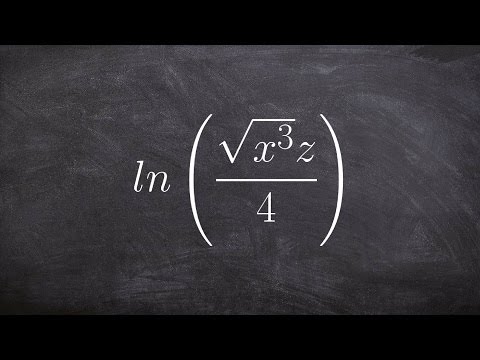 0:04:44
0:04:44
 0:03:51
0:03:51