Vitali Set and Vitali Theorem

The video shows that the approach to measures and integration explained in the previous video does not work for large class of measures. This explains why the measure and integration requires a more refined approach.

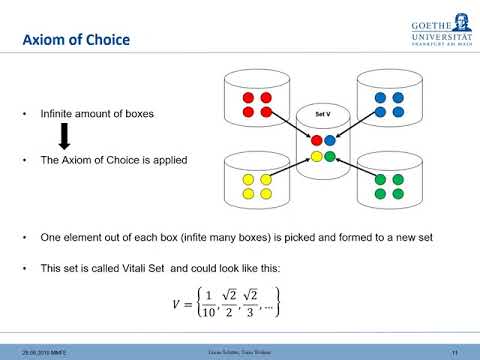
Also, in the language of measure and integration, the video shows that there are non-measurable sets. The Vitali Set is an example of such set.

[alditoify]

This video was very good at motivating measure theory!. I've always seen positive examples of measures but negative examples are needed to let you truly get why do we need measure theory.

[wesleyrm]

Really thorough explanation! You need to prove the equivalence classes are disjoint, no? Because otherwise you can't make a 1-to-1 correspondence between the x's and their equivalence classes S_x. Sorry, I just randomly bumped in this video, maybe this is assumed to be trivial in the study of equivalence classes.

This is what I thought as a proof:
If z is in S_x and S_y, z is equivalent to x and y at the same, so x and y should also be equivalent, since the equivalence relation can be shown to be transitive (Difference of rationals is also rational). So, if x and y aren't equivalent, the intersection of S_x and S_y is empty, otherwise we would have a contradiction, since there would exist such a z.

If x and y are equivalent, S_x = S_y. The negation of this statement is: if S_x and S_y are different, x and y can't be equivalent.
As we have shown, if x and y aren't equivalent S_x and S_y have empty intersection.
This means that if S_x and S_y are different, they have empty intersection as well.
That is, each S_x can be uniquely described by a single one of its elements.

[hayallerimverenklerim]

Nice but English 😀 I’m Turkish who studying Proffesional English (in mathematics) at university second class department of mathematics I wish a day well speak English (can be my mistakes about this sentence because only I wrote no help translate) for now A2 level English. Thank you so much for this detailed mathematics video.

[thekolbaska]

It is not at all obvious that the interval [0, 1] is contained in the union of V+r over all rationals r. Also, I assume that we're looking at not only rationals, but specifically rationals r such that  |r|<1? Otherwise the union would not be contained in the interval [-1, 2]. Does anyone know how to show that we cover the entire interval [0, 1]?

[MariusHofert]

Denis Potapov : Hi, what program do you use to display the formulas (besides LaTeX behind the scenes)?

[alexandredamiao]

Great video!! Thanks for the exposition! (By the way, this software you used to show the equations looks very nice. I noticed some stuff from latex. What is it's name?)

[pavybez]

Thanks Denis for the great video. I fail to understood where the lemma is used in the final proof. Could you please help?

[Oja]

nice work. where can i find the software you use. thanks