Chapter 20. Lagrangian and Hamiltonian mechanics (Part 1)

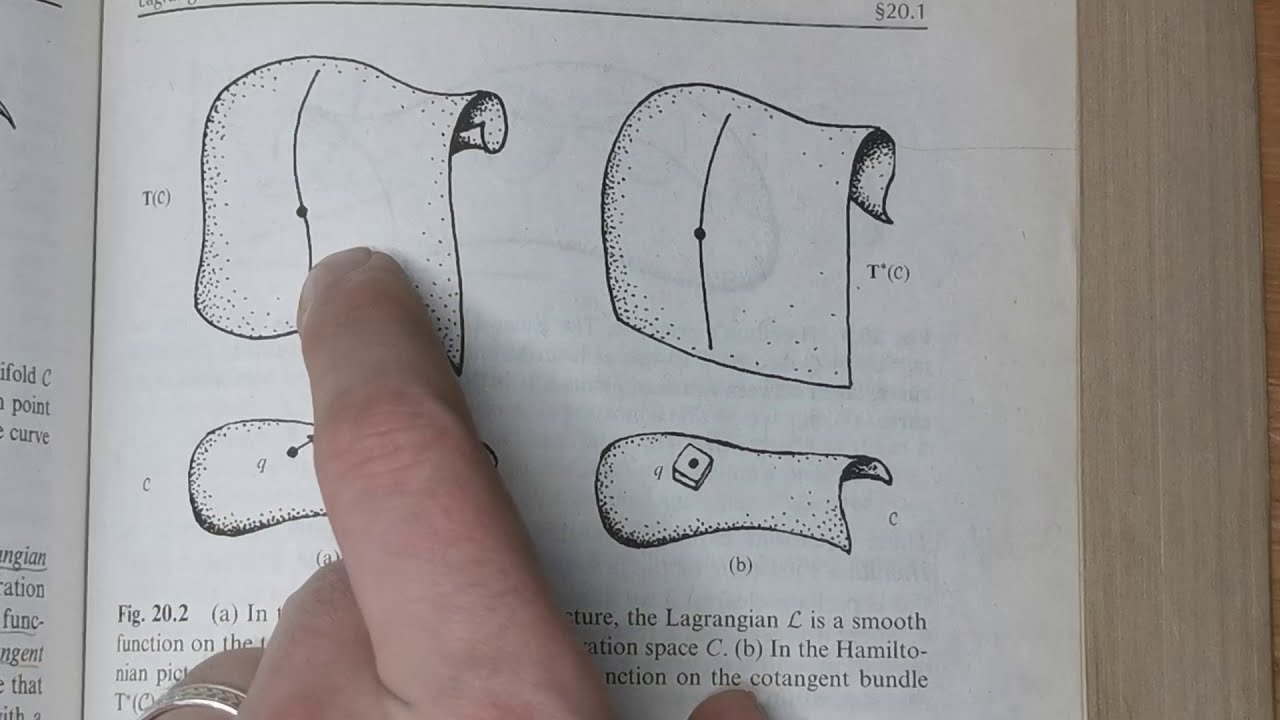
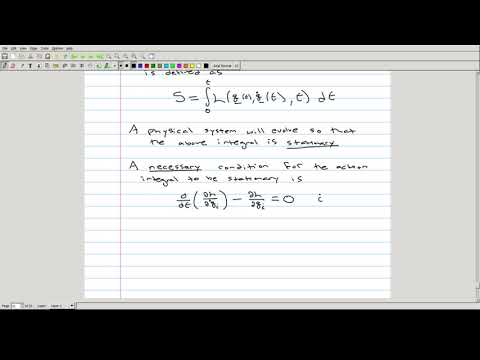
Here we talk about 20.1 - 20.3.
Additional literature:

1. Landau, Lifshitz - Mechanics. Is a pretty straightforward introduction to the matter. I suggest reading the first two chapters. (sometimes you will feel that you need some explanations, authors were probably thinking that you should work on a full-fledged explanation by yourself). Anyway - it contains a great intro about Lagrangians, their independence of scaling and full-time derivatives, and connection of the v^2 dependence to the homogeneity of space and time and isotropy of space.

2. Gelfand, Fomin - Calculus of Variations. Detailed mathematical approach. With physical examples as exercises (solved for you).

3. Susskind, Hrabovsky - Theoretical Minimum. Probably the easiest and the lightest introduction into a subject.