Complex Network Growth And Chaos From A Simple Rewrite Model

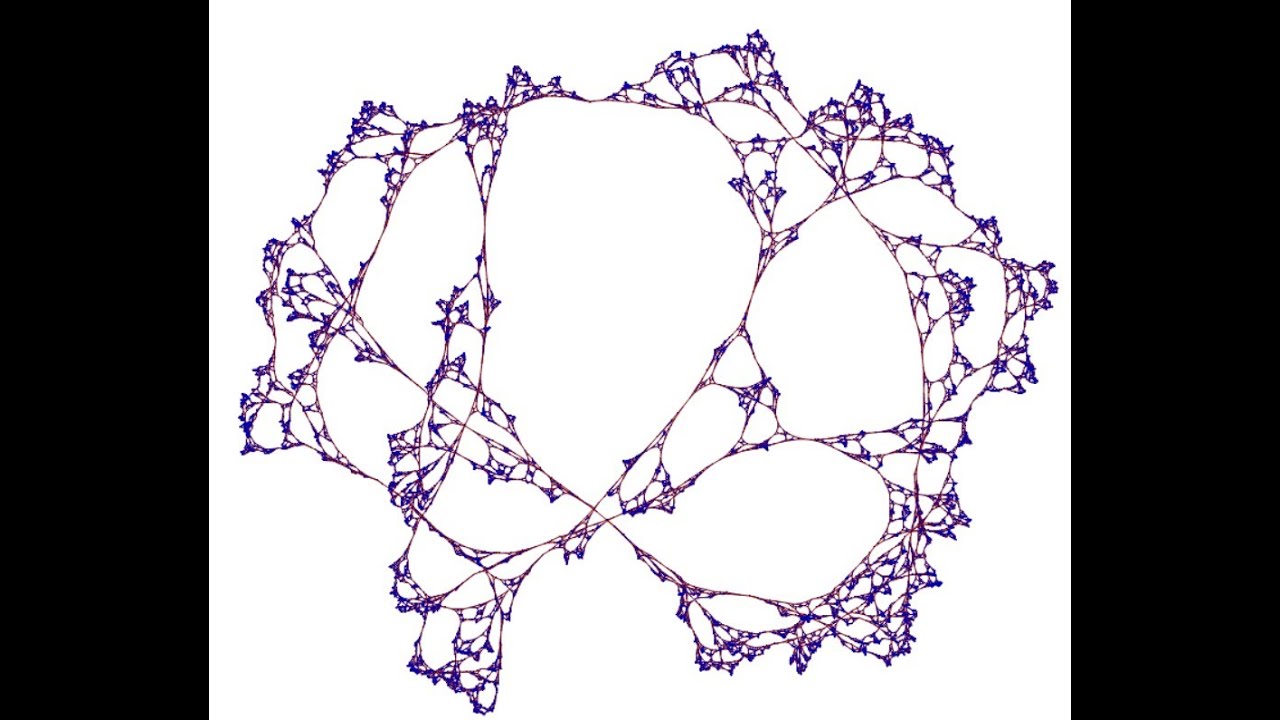
We describe a simple network rewrite model which generates a highly complex network. The system works a little like a Turing machine, in the sense that there is a `writer' which moves around the network and performs local deterministic rewrite operations (complete system description at bottom).

In other works we have looked at these systems in a more general way:

Complex Networks, Simple Rules

Searching For Complex Systems - Live

Complex Networks from Simple Rules (paper)

But here we focus on a particularly interesting system. Even when we evolve the system for 1000000 time steps, the structure produced remains highly intricate. Although some self-similar structures seem to appear in different locations, there is an overall heterogeneity about the system, as the writer's movement seems unpredictable.

We show the system evolving im real time for the first 300 time steps, and then perform some deep statistical analysis to determine whether the behaviour produced is truly complex or not.

Although the growth rate of the number of vertices is very closely
linear, the deviation between the actual number of vertices and the
predicted-number (via a linear best fit) looks extremely complex.

We plot how the position of the writer changes over time. These seems remarkably complex. Indeed, it seems difficult to find any discernible pattern. However, there does seem to be phase transitions of a sort. At roughly time step 90000 the writer seems to stop regularly visiting the only initial vertices, and starts visiting a set of other vertices with greater frequency.

In each of our studies we found a lack of discernable pattern. In `A New Kind Of Science' Stephen Wolfram makes the important distinction between `chaotic systems' (where pseudo-randomness is widespread), and `complex systems' (which seems to involve a mixture of order and chaos, and often have persistent substructures which interact).

Our results suggest that this network growth system is chaotic, as
oppose to complex. However, we obviously have no proof that our system is chaotic (via Devaney's criteria).

Formally our system can be described verbally as follows:

We start with a cube, one vertex of which is black, and called the
writer. There are exactly three (undirected) edges touching each vertex of our graph, one of which is red, one of which is blue and one of which is green. Our system is defined by 4 rewrite rules, which can be described verbally as follows:

If there are no edges linking the writer's neighbors (case 1) then the writer moves along a blue edge, then a red edge, and its previous position is replaced by a triangle.

If there is exactly one edge between the writer's neighbors, which is red (case 2), then the writer just moves along a blue edge, and makes no structural alterations.

If there is exactly one edge between the writer's neighbors, which is blue (case 3), then the writer moves along a red edge, and then replaces its previous position with a triangle.

If there is exactly one edge between the writer's neighbors, which is green (case 4), then the writer moves along a green edge T1 move (see `A New Kind of Science', Stephen Wolfram, Page 1038) is performed, which `switches' the green edge just traversed.

You can explore the system yourself using the Wolfram Demonstration

[RichardSouthwell]

How to make amazing amounts of chaos and complexity using a super simple rule (plus I'm getting a 3D print of the resulting complex network soon, happy days :)