Boundary Conditions of the Wave Equation - Partial Differential Equations | Lecture 19

preview_player
Показать описание
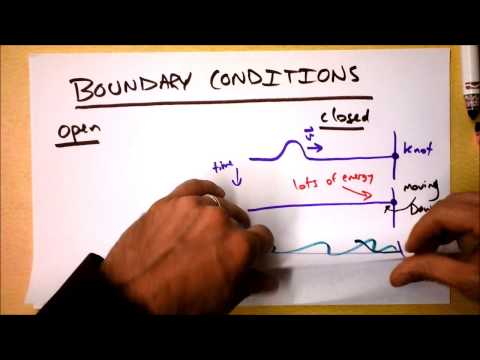
Now that we have derived a new PDE, we need to consider appropriate boundary conditions. In this lecture we discuss and derive boundary conditions for the 1-dimensional wave equation describing vibrations of a string. An interesting set of boundary conditions comes from considering one end of the string attached to a vibrating spring-mass system. In this case we find that the boundary condition becomes analogous to Newton's law of cooling for the heat equation.

Follow @jbramburger7 on Twitter for updates.
  1. Jason Bramburger
  2. partial
  3. differential equation
  4. pde
  5. ode
  6. ordinary
Рекомендации по теме
PHYS 201 | 0:07:05

PHYS 201 | Wave Interface 4 - Boundary Conditions

2D Wave Equation 0:00:17

2D Wave Equation Simulation - Dirichlet Boundary conditions

2D Wave Equation 0:00:17

2D Wave Equation Simulation - Neumann Boundary conditions

Electromagnetic Boundary Conditions 0:11:26

Electromagnetic Boundary Conditions Explained

Boundary Conditions for 0:04:43

Boundary Conditions for Wavefunctions

2D Wave Equation 0:00:17

2D Wave Equation Simulation - Absorbing Boundary conditions

What Happens When 0:04:29

What Happens When Waves Reflect | Doc Physics

Boundary Conditions — 0:05:59

Boundary Conditions — Lesson 7

Boundary conditions of 0:03:11

Boundary conditions of one dimensional wave equation

40-Boundary conditions on 0:22:46

40-Boundary conditions on the wave equation

Explain Boundary conditions 0:05:08

Explain Boundary conditions of Standing Wave. | Basic Quantum Chemistry

1D Wave Equation: 0:00:17

1D Wave Equation: Open Boundary Conditions

Boundary conditions reflection 0:01:04

Boundary conditions reflection

Boundary Conditions of 0:17:14

Boundary Conditions of the Wave Equation - Partial Differential Equations | Lecture 19

Lecture 25.2 - 0:08:19

Lecture 25.2 - Boundary Conditions on Standing Waves

Reflection and Transmission 0:31:31

Reflection and Transmission of Transverse Waves

MM58: Dirichlet and 0:10:48

MM58: Dirichlet and Von Neumann BC

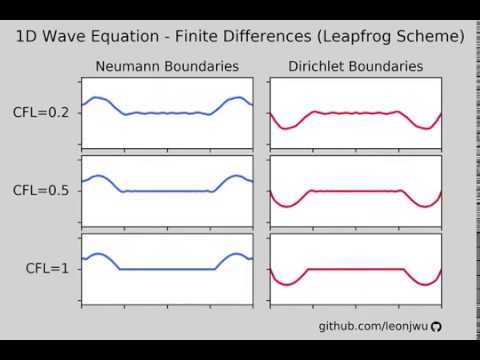
1D Wave Equation 0:00:34

1D Wave Equation with Different Boundary Conditions and CFL Numbers

Boundary conditions 0:03:26

Boundary conditions

University Physics Lectures, 0:09:35

University Physics Lectures, Waves Under Boundary Conditions

Simulation of inhomogeneous 0:00:31

Simulation of inhomogeneous acoustic wave equation with absorbing boundary conditions (free on top)

Haberman 4.3 - 0:18:24

Haberman 4.3 - Boundary conditions for the wave equation

Physics - Ch 0:04:23

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (82 of 92) Barrier: Boundary Conditions

PHYS 201 | 0:04:59

PHYS 201 | Traveling Wave 6 - Boundary Conditions

Комментарии
Автор

would you mind helping me solving wave equation in higher dimension with initial, boundary or sourse is defined by a step function by making more video in this serie for that. I'm very comfortable with 1D-wave equations and condition is just a continous function like g(x) or h(x) but that problem makes me sick on my exam

hainguyenle