filmov
tv
Algebra 56 - A Geometrical View of Gauss-Jordan Elimination
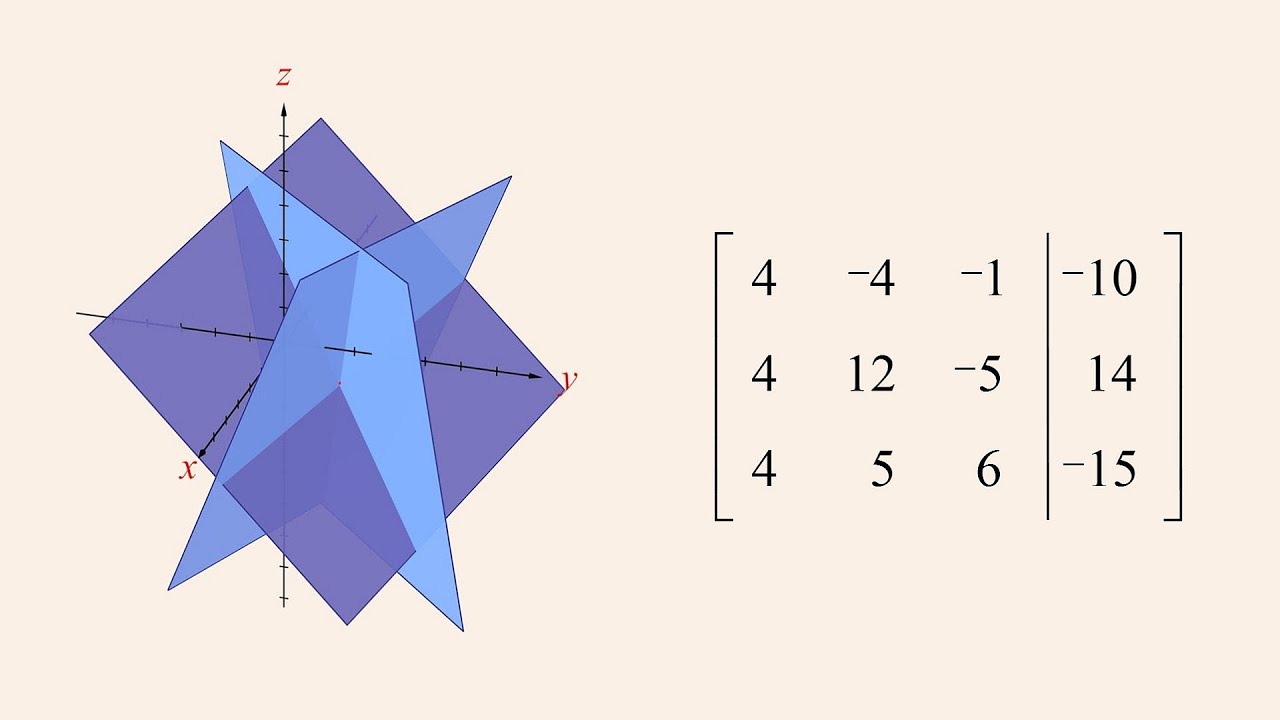
Показать описание
Although Gauss-Jordan Elimination is typically thought of as a purely algebraic process, when viewed geometrically, this process is beautiful and amazing, providing insights into the underlying mechanisms of the matrix transformations which lead to the solutions of a system of linear equations. Since a system of linear equations in three variables is graphically represented by a collection of planes, following how these planes change their orientation with each row operation can give us an intuitive understanding of how the transformation to reduced row echelon form works.
Algebra 56 - A Geometrical View of Gauss-Jordan Elimination
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Addendum to A Swift Introduction to Geometric Algebra
Saxon Algebra 2 - Lesson 56 - Angles in Circles
Counterexamples in Geometric Algebra
Commutative algebra 56: Hilbert polynomial versus system of parameters
Maths Tutorials | Algebra | GEOMETRIC PROGRESSION | part-4 | Article 56 | Hall & knight
Algebra 1 Absolute Value Equations: 7|n|=56 (Quick Math Videos)
Similar Triangle | BPT Proof | Maths Xth Chapter 6 | Live Class
Algebra 48 - A Geometrical View of the Elimination Method
Calculate the area of the shape | Important Geometry and Algebra skills explained
Every Student Should See This
Calculate the distance AB | Important Geometry and Algebra skills explained
what is this.#algebra#confusing#memes
Changing the Subject_P1 in 56seconds😊. #viral #reels #subject #change #algebra #geometry #eq
Memorization Trick for Graphing Functions Part 2 | Algebra Math Hack #shorts #math #school
Solve a linear inequality. #math #algebra #geometry #algebra2 #inequalities
Saxon Math - Pre-Algebra 1/2: 3rd Edition (Lesson 56) - Equations with Mixed Numbers
Algebra and Triangles : solving equations linked to perimeter and area
Unique Algebra Problem – Always Try Something to Solve
Can you find the area of the Yellow shaded triangle? | (Circle) | #math #maths | #geometry
Algebra for Beginners | Basics of Algebra
SAXON ALGEBRA 2 | LESSON 56
Solution of two line intersection using geometric algebra.
Комментарии
 0:13:42
0:13:42
 0:00:15
0:00:15
 0:23:40
0:23:40
 0:07:05
0:07:05
 0:00:57
0:00:57
 0:09:20
0:09:20
 0:04:51
0:04:51
 0:00:35
0:00:35
 0:21:20
0:21:20
 0:13:52
0:13:52
 0:04:01
0:04:01
 0:00:58
0:00:58
 0:09:15
0:09:15
 0:00:06
0:00:06
 0:00:57
0:00:57
 0:00:13
0:00:13
 0:00:48
0:00:48
 0:04:31
0:04:31
 0:01:53
0:01:53
 0:10:21
0:10:21
 0:08:56
0:08:56
 0:37:09
0:37:09
 0:17:35
0:17:35
 0:07:22
0:07:22