Nested Interval Property and Proof | Real Analysis

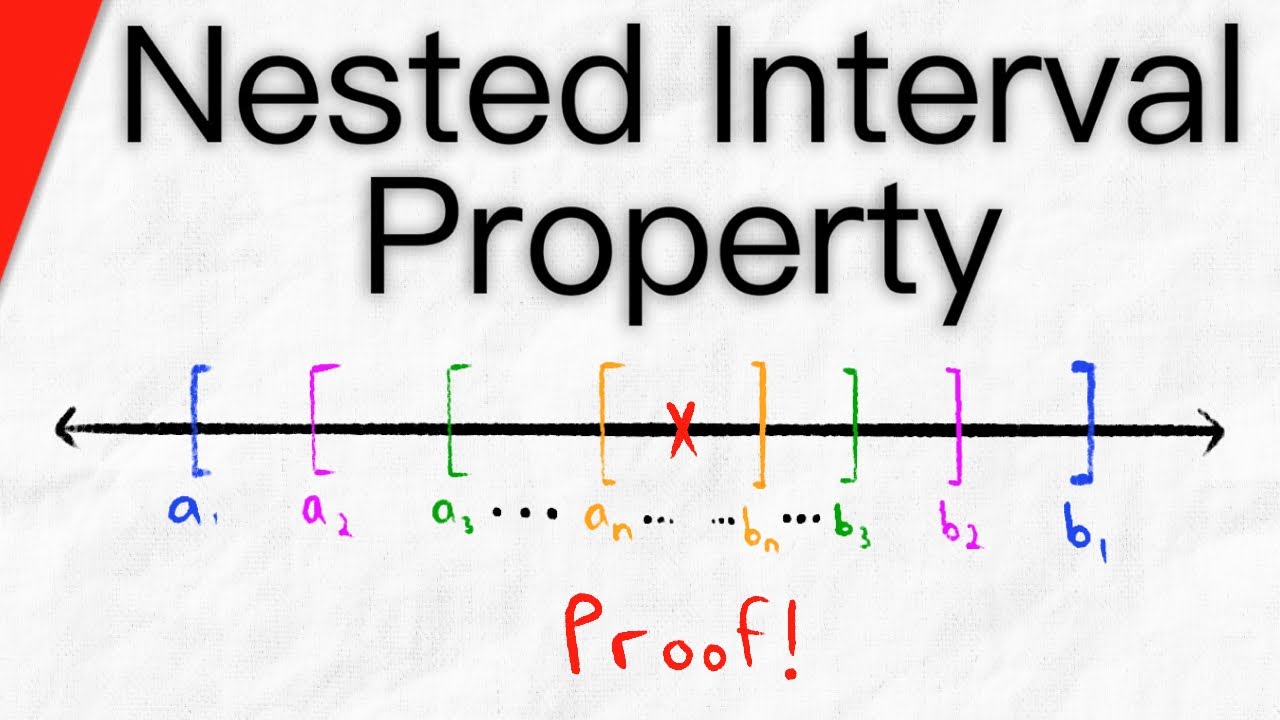
We introduce and prove the nested interval property, or nested interval theorem, or NIP, whatever you like to call it. This theorem says that, given a sequence of nested and closed intervals, that is, closed intervals J1, J2, J3, and so on such that each Jn contains Jn+1, this infinite sequence of nested intervals has a nonempty intersection. We prove this using the axiom of completeness and a supremum. #RealAnalysis

Axiom of Completeness: (coming soon)

◉Textbooks I Like◉

★DONATE★

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Follow Wrath of Math on...

[WrathofMath]

Support the production of this course by joining Wrath of Math to access exclusive and early videos, original music, plus the real analysis lecture notes at the premium tier!

[Joshs]

bro deserves much much more views, pls keep making more videos on analysis, love from Colorado❤

[thunayyanhussam]

I never get disappointed watching your videos! Always very informative and well delivered. Please keep on you are the best math tutor on YT!

[jscotch]

Still helping people even now! Thanks so much it was sooo much easier to understand!

[suhanisoni]

Very very informative video, literally saved my life. Thank you so much

[mfonpeter]

I love the way you explained the concept, making use of genius and simple examples. Keep up the good work 👍.

[apratick]

You are a legend. Wish you all the success in life. Will definitely support you after I start earning.

[chelekakaumba]

My exam is one week away, I find your videos very helpful. ♥️

[punditgi]

A very important and informative video!

[himanshukumarr]

Your videos are coolest, Helped me in exams

[adityasethy]

Most lucid explanation of the Nested Interval Theorem

[gonzajuarez]

Hey. Thanks for the video. I've been stuck at this for a couple of hours. One question though. Why doesn't this proof consider the case where one of the nested intervals is the empty set. My best guess is that this has to do with it being about an *infinite* sequence of closed nested sets. But again, the empty set is included in itself so it could go on and on and on and... on.

If the empty set is considered in the sequence, then such x wouldn't exist. As per my understanding.

[mathmaniaa]

nice video, thx for upload this... may I ask...how to create the nested set so the intersection is (-2, 1]

[vinwithaw]

Question, how does this prove that the real no. Line has no holes? If x belongs to the closed interval [a_n, b_n], then that could imply that x CAN be equal to a_n or b_n, thereby producing a hole between a_n and b_n?

[siriuss_]

Hey WoM, any case where that x can be a set (finite), I cant find such Example and my stupid brain is getting more inclined towards a singleton set

[okikiolaotitoloju]

Could we have used an infimum instead of a supremum for x?

[ericoduroboateng]

please, it is always given in a closed interval?