filmov
tv
If n is a composite positive integer then n divides (n - 1)! except when n = 4 (1001-180)
Показать описание
Let n be a positive integer. Show that if n is a composite integer then n divides (n - 1)! except when n = 4
#numbertheory #composite #integer #cipher
#numbertheory #composite #integer #cipher
0:02:47
Discrete Math - Proof - Composite integer n has divisor less than sqrt(n) (Request)
0:01:53
If n is a composite positive integer then n divides (n - 1)! except when n = 4 (1001-180)
0:02:55
(NUMBER THEORY) Lecture 14: if n is composite, then the smallest prime divisor of n less than sq (n)
0:03:23
(n-1)! is multiple of n when n≠4 is composite, in contrast to Wilson's Theorem for prime number...
0:02:20
A composite number n has always a prime factor not exceeding root n
0:36:31
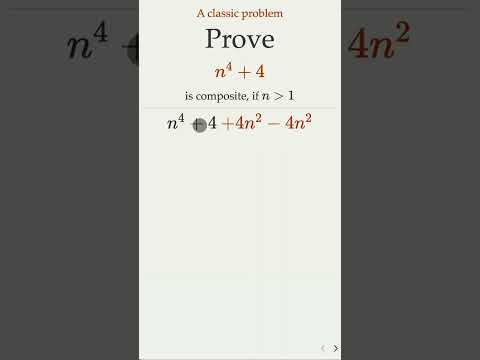
Prove that n^4+4 is composite if n is greater than 1.
0:01:32
Show that 111- - -11(n digits, all ones) is composite if n is composite, is the converse true?
0:01:00
Prove n^4+4 Is Composite
0:05:53
NUMBER THEORY: Proof of composite integer n has prime factor not exceeding √n
0:05:04
Suppose n is a composite natural number, Prove 2^n - 1 is also composite
0:02:31
If m is prime, n is a composite number and `m+ n=240` also their LCM is 4199. Find m and n.
0:04:59
Theorem: Every composite integer x contains a prime factor less than equal to its square root
0:04:37
n⁴+4^n // prime // composite // Number Theory8 Chemaths Risers
0:07:22
Sigma Function | Examples | If n is composite number then show sigma (n) is greater than n + n^1/2.
0:09:11
Given any integer n we can find n consecutive composite integers .
0:05:06
Is a Number Prime or Composite? (Math for Teachers)
0:02:36
Is 1 a Composite Number? (Why isn't 1 Composite?)
0:11:47
Proof that one less than a square number is composite (not prime)
0:03:51
Does every arithmetic sequence have an arbitrary long number of consecutive composite members?
0:02:37
Solving using Wilson's theorem and definition of composite numbers (AITTTON-2.1-35)
0:09:44
Establishing n^4 + 4^n is composite without using Sophie Germain algebraic Identity
0:11:29
Euler’s Phi Function | Examples | If n is a composite number then phi (n) = n-n^1/2 | Lecture-8
0:04:40
Recognizing prime and composite numbers | Factors and multiples | Pre-Algebra | Khan Academy
0:01:00
When Can A Composite Function Exist? | A-Level H2 Math, Singapore
Комментарии