Mercury of density \( \left(\rho_{\mathrm{Hg}}\right) \) is poured into cylindrical communicatin...

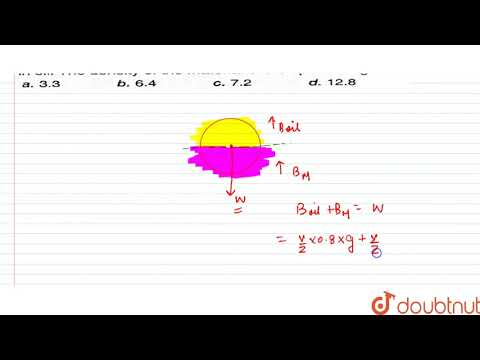
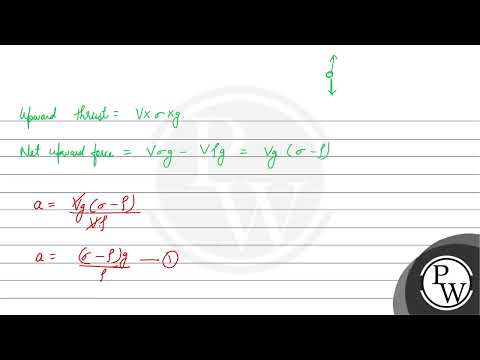
Mercury of density \( \left(\rho_{\mathrm{Hg}}\right) \) is poured into cylindrical communicating vessels of cross-sectional area \( A_{1} \) and \( A_{2} \) respectively \( \left(A_{1}A_{2}\right) \). A solid iron cube of volume \( V_{0} \) and density \( \rho_{\text {iron }} \) is dropped into the broad vessel, and as a result the level of the mercury in it rises. Then liquid of density \( \rho_{\text {liq }} \) poured into the broader vessel until the mercury reaches the previous level in it. The height of water column \( h \) is :
(a) \( \frac{V_{0} \rho_{\text {iron }}}{\rho_{\text {liq }}\left(A_{2}+V_{0}^{2 / 3}\right)} \) if the liquid does not submerge the block
(b) \( \frac{V_{0} \rho_{\mathrm{iron}}}{\rho_{\mathrm{liq}} A_{2}} \) if the liquid does not submerge the block
(c) \( \frac{V_{0}}{A_{2}} \) if the liquid submerge the block
(d) \( \frac{V_{0}}{A_{2}}\left(\frac{\rho_{\text {iron }}-\rho_{\mathrm{liq}}}{\rho_{\mathrm{Hg}}-\rho_{\mathrm{liq}}}\right) \frac{\rho_{\mathrm{Hg}}}{\rho_{\mathrm{liq}}} \) if the liquid submerge the block