filmov
tv
The Generalized Likelihood Ratio Test

Показать описание
There is no universally optimal test strategy for composite hypotheses (unknown parameters in the pdfs). The generalized likelihood ratio test (GLRT) is a likelihood ratio in which the unknown parameters are replaced by their maximum likelihood estimates. Example of the GLRT for detecting a signal of known shape but unknown amplitude in noise of unknown variance.
The Generalized Likelihood Ratio Test
Likelihood ratio test - introduction
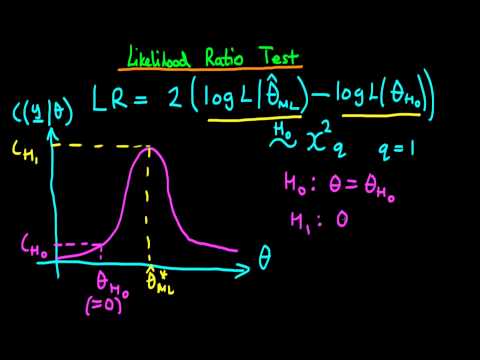
Lecture 18: Generalised Likelihood Ratio Test
6 3 Generalised Likelihood Ratio Tests (Part 1)
Likelihood Ratio Tests Clearly Explained
Lec 14: Generalized Likelihood Ratio Testing
Math218 Lecture 6.2 Likelihood Ratio Tests 2
Wald test | Likelihood ratio test | Score test
6.6 Likelihood Ratio Test (LRT) in R
STAT 510 /// Likelihood Ratio Test Examples
Nested model comparison with likelihood ratio test
452 S21 Lecture 20 - Likelihood Ratio Test
6.5 Likelihood Ratio Test (LRT) Explained
Likelihood Ratios Explained
The Likelihood Ratio Test
Likelihood Ratio Test for Exponential Distribution by Mr. Rohit Gupta | IXPOE
Kelompok 10 - Generalized Likelihood Ratio Test
W2D3 Decision Making Tutorial 1 Part 1
Likelihood Ratio
Likelihood Ratio Test
What Are Likelihood Ratios and How Are They Used
Liklehood ratio test
Lecture 12.8 - Hypothesis testing: Likelihood ratio tests
Maximum Likelihood, clearly explained!!!
Комментарии
 0:14:07
0:14:07
 0:06:10
0:06:10
 0:17:52
0:17:52
 0:16:57
0:16:57
 0:18:28
0:18:28
 1:45:35
1:45:35
 0:10:30
0:10:30
 0:13:30
0:13:30
 0:04:18
0:04:18
 0:21:54
0:21:54
 0:03:14
0:03:14
 1:11:09
1:11:09
 0:03:40
0:03:40
 0:08:19
0:08:19
 0:16:40
0:16:40
 0:07:04
0:07:04
 0:12:56
0:12:56
 0:04:46
0:04:46
 0:03:09
0:03:09
 0:17:58
0:17:58
 0:10:10
0:10:10
 0:05:49
0:05:49
 0:18:49
0:18:49
 0:06:12
0:06:12