filmov
tv
Approximating (1.998)^4 by using differential

Показать описание
Approximating (1.998)^4 by using differential,
Please subscribe for more calculus tutorials and share my videos to help my channel grow! 😃
Comment #YAY down below & your comment might be featured in my future videos!!!
Check out my site & social media
Thank you for watching!
blackpenredpen | 曹老師
Please subscribe for more calculus tutorials and share my videos to help my channel grow! 😃
Comment #YAY down below & your comment might be featured in my future videos!!!
Check out my site & social media
Thank you for watching!
blackpenredpen | 曹老師
Calculus I - Linear Approximations and Differentials
Salsa Night in IIT Bombay #shorts #salsa #dance #iit #iitbombay #motivation #trending #viral #jee
Simplify i^(23) Complex Numbers #shorts
MATH I: Linearization and Differentials Arabic Narration
Solving Simple Differential Equations | Specialist Mathematics | TI-Nspire CX CAS
Limits Calculator Technique
Linearization and Differentials
Differential Equations, Slope Fields and Euler’s Method | Specialist Mathematics | TI-Nspire CX CAS...
Behind the Scene of the Class after becoming Parents || Work Life Balance ||
Integration and forgot to +C (Math meme)
Section 4 8 Differentials Part II
How to Evaluate i to a Negative Exponent: Example with i^(-23) #shorts
Chapter 1.5 Problem 3 (Advanced Engineering Mathematics)
Using Differentials find the Approximate Value of f(x)- 🕉 Maths corner by Yash Pal sir
Errors in Numerical calculations
AP Calc BC 2023 FRQ #1
11.10 *BONUS* Approximating Pi using Taylor Series
Applications of Differential Equations | Specialist Mathematics | TI-Nspire CX CAS
Jacobi Iterative Method
2.APPLICATION ON DERIVATIVES, CLASS 12 TH / HSC/ MHTCET, LECTURE 6 approximations
Basic Differential Calculus | Mathematical Methods | TI-Nspire CX CAS
BT: Negative & fractional indices: SE8 Binomial approximation of (n+1)p+(n-1)q/(n-1)p+(n+1)q
Application of Derivative(Approximation Part-1)solved Examples
Harvard AM205 video 3.13 - Stiff ODE systems
Комментарии
 0:51:27
0:51:27
 0:00:14
0:00:14
 0:00:43
0:00:43
 0:22:16
0:22:16
 0:32:09
0:32:09
 0:01:49
0:01:49
 0:59:28
0:59:28
 0:21:49
0:21:49
 0:00:19
0:00:19
 0:00:09
0:00:09
 0:42:31
0:42:31
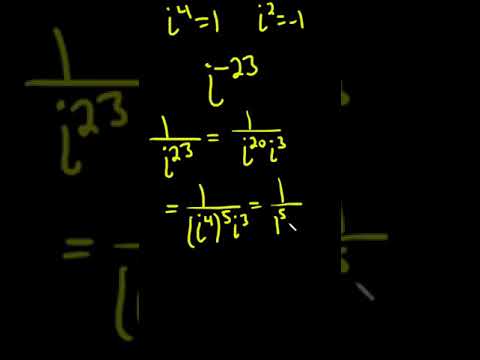 0:01:01
0:01:01
 0:06:53
0:06:53
 0:39:51
0:39:51
 0:12:52
0:12:52
 0:10:43
0:10:43
 0:22:28
0:22:28
 0:34:53
0:34:53
 0:19:01
0:19:01
 0:37:18
0:37:18
 0:36:25
0:36:25
 0:02:35
0:02:35
 0:38:05
0:38:05
 0:15:51
0:15:51