filmov
tv
Riemann Roch: structure of genus 1 curves

Показать описание
This talk is about the Riemann Roch theorem in the spacial case of genus 1 curves or Riemann surface. We show that a compact Riemann surface
satisfying the Riemann Roch theorem for g=1 is isomorphic to a nonsingular plane cubic. We show that this is topologically a torus, and use this to show that it can be represented as C/L for a lattice.
This video is based on a discussion section of an online algebraic geometry course.
satisfying the Riemann Roch theorem for g=1 is isomorphic to a nonsingular plane cubic. We show that this is topologically a torus, and use this to show that it can be represented as C/L for a lattice.
This video is based on a discussion section of an online algebraic geometry course.
Riemann Roch: structure of genus 1 curves
Applications of Riemann-Roch to Classifying Low genus curves
The Riemann-Roch Theorem for Surfaces
Riemann Roch: genus 1
Riemann Roch for genus 0 curves
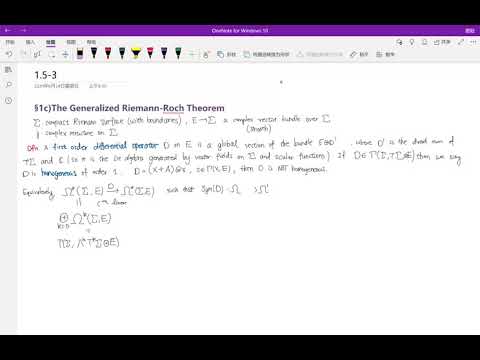
[ISS, Fall 2022] Lecture 4 - Riemann-Roch Theorem
Riemann Roch Spaces
What is...the Riemann-Roch theorem?
Analytic Grothendieck Riemann Roch Theorem || Prof. Xiang Tang || WOTOA
Riemann Roch: plane curves
Example: Hirzebruch-Riemann-Roch for threefolds
The Riemann-Roch theorem for curves
Riemann-Roch Theorems | Cohomology in Algebraic Geometry - Anton Fonarev (Part 4)
Riemann Roch (Introduction)
Riemann-Roch
14.2 The statement of the Riemann-Roch Theorem (Commutative Algebra and Algebraic Geometry)
Example: Hirzebruch-Riemann-Roch for Surfaces
'Riemann–Roch spaces and algebraic geometry codes' - Elena Berardini
Weronika Czerniawska: “Unifying global theory for the Riemann-Roch theorem in low dimensions”
Riemann Roch if space is a single point
Philipp Habegger: The Number of Rational Points on a Curve of Genus at Least Two
seminars on Riemann-Roch theorem 2
Genus of a curve --- CAG L21
Motivation (part 2) Period Matrix of a Riemann Surface of Genus g
Комментарии
 0:18:05
0:18:05
 0:25:09
0:25:09
 0:19:07
0:19:07
 0:31:37
0:31:37
 0:21:14
0:21:14
![[ISS, Fall 2022]](https://i.ytimg.com/vi/AuxvP6eQ-1g/hqdefault.jpg) 1:04:39
1:04:39
 0:10:21
0:10:21
 0:10:10
0:10:10
 1:00:47
1:00:47
 0:23:19
0:23:19
 0:15:02
0:15:02
 0:20:13
0:20:13
 1:45:05
1:45:05
 0:27:38
0:27:38
 0:03:56
0:03:56
 0:16:09
0:16:09
 0:06:56
0:06:56
 0:20:23
0:20:23
 0:56:39
0:56:39
 0:17:45
0:17:45
 0:45:15
0:45:15
 1:26:13
1:26:13
 0:14:34
0:14:34
 0:06:51
0:06:51