State and Action Values in a Grid World: A Policy for a Reinforcement Learning Agent

** Apologies for the low volume. Just turn it up **
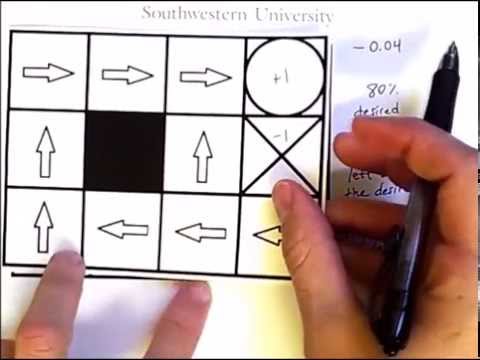
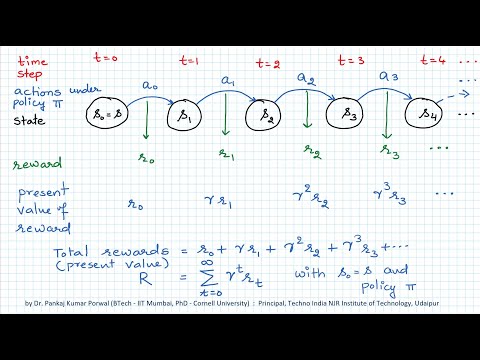
This video uses a grid world example to set up the idea of an agent following a policy and receiving rewards in a sequential decision making task, also known as a Reinforcement Learning problem. Although there is no learning agent yet in this video, the concepts of state values (utility) and Q-values are discussed, which are vital components of many RL algorithms. The grid world formulation comes from the book Artificial Intelligence: A Modern Approach, by Russell and Norvig.

[himanshutalegaonkar]

i have gone through multiple articles, but you sir have the most precise and easy to understand explanation!!! thanks!!

[Skandawin]

you didn't mention how you arrived at 0.660 in first place

[Grkashani]

Jacob you were brilliant, No boduy else explained like you, as Albert Einstein said : If you can't explain it simply, you don't understand it well enough

[whilewecan]

Wonderful. I understood. I had difficult time understanding with other articles. Thank you very much.

[engineered.mechanized]

Excellent explanation. Cant appreciate enough how easy you made it to understand.

[alexandrulita]

Jacob, great series, I enjoyed every minute!

[robthorn]

One thing I really like about this video is that it included numeric examples which allow me to try the process for myself and verify that I am doing it correctly by matching the numbers. For example, the values shown at 4:47. I am able to duplicate these numbers according to the process shown at time 7:00. However when I code this into a PHP program, I do not get the same values and further, I don't even get the same path.

My program chooses the bottom route, completely ignoring the danger of falling into the trap on the right side middle state. On examining the process, it is clear that more is going on than the simple application of the Bellman equation. What I was doing was selecting an action by taking the optimum 80% of the time and a left or right variant 10% each. Then I applied the Bellman equation. But what I'm seeing is that the wrong Q(s, a) is getting updated. Next I tried updating the Bellman equation for the optimum action even though I didn't take that route. The results were better, the upper route was selected, but the calculated values are nothing like those in the video.

My question is this: how do epsilon-greedy and Bellman work together in the RL example given? How can we run the program and expect to get result like those in the video?

[unitynofear]

5:00 the values don't seem to match the policy. It seems agent when on bottom right 0.611 square should choose top square instead of left; 0.660 > 0.655
In other words, following the policy will bring you more utility in the long run from the upper square, it's therefore more desirable to go up, so the policy that maximizes the utility should be updated according to the numbers.
Of course, the policy can choose smaller value actions. But then how is that a match?

[saketdeshmukh]

how could you subtract .04 only once in the equation ? Each action has the cost .04 ? how would equation look like if the cost is different to move in different direction ?

[tomm]

Wouldn't the agent want to move left towards the wall (therefore remaining in place) when it is between the wall and the negative reward square? Since it will never move in the opposite direction of it's intention, it can repeatedly walk into the wall until it moves sideways.

[AnAyahaDay]

Sir, do you have a lecture on Q-learning with a linear function approximator (based on the features) to train the Q-function ??? To solve MountainCar problem
, or can be other as well

[ferminquant]

Great series, very well explained. After making this GridWorld and playing with it, I noticed that what you say at around 4:27 does not hold true for me. You state that the two left arrows on the bottom in the middle columns, that they are left because it is dangerous to accidentally fall into the -1 terminal state. And you walk trough the math on why, which make sense.
However the QLearning formula does not take into account all possibilities of the next state, it only considers the max value. After letting run my GridWorld it converges into taking that dangerous path you mention when in those positions, because it is the one with the most rewards, ignoring any danger of falling to the -1 state.
Is this by design of QLearning? Are there other algorithms that do take this into consideration? If so, how do they deal with a changing epsilon value through time, as it would change the QValues every time epsilon changes?

[ShivamRaj-dtzm]

the ai.berkeley link is not working please upload the files in drive and share link

[shivanishah]

The explanation is really good. However, how do you start the entire process? With what value should the states be initialized?

[Skandawin]

how did you set up the movement cost as -0.04 ?

[EduardoYukio]

Awesome explanation! For some reason I didn't understand well neither with my teacher nor my book, but your channel is working!

[jhonlu]

how can i calculate this trial ?
(1, 1)-> (2, 1) ->(3, 1)-> (3, 2)-> (3, 3)-> (4, 3) ?

[maulikmadhavi]

Great video! What is the difference between state value and Q value?

[rursus]

If I was that flawed wandering machine, I would go to the left if I was in row2-column3 cell. 80% of the time I would bounce of the wall, but 10% I would go to row3-column3, and 10% I would go to row1-column3, none of them fatal.

[robthorn]

After long study and much experimentation, I have concluded that this description of Q-learning is WRONG. The numbers just don't check. But more fundamentally the way the grid world is defined AND the way the epsilon-greedy policy are described are WRONG. In particular, when the reward is received (when we enter the upper-right square) is contrary to the standard usage, i.e., when we leave a state. Further, it is very vague whether this upper-right square is a terminal state or not. If these anomalies don't make it wrong, they at least are very confusing. Then there's the random (exploration) moves: The typical usage of epsilon is to specify a probability that a random action, i.e., any of the four possible states, will be taken. In this video the random policy is unnecessarily complicated.

I have just finished watching a 10-video series on Reinforcement Learning by David Silver and, besides being too long, about 16-17 hours total, and mind-numbingly repetitive, it is consistent and the algorithms provided actually work. There are others, from MIT, etc., well worth watching but this one from Dr. Schrum is misleading. Sorry doc.