Introduction to Graph Data Structure - Graph Properties & Terminologies

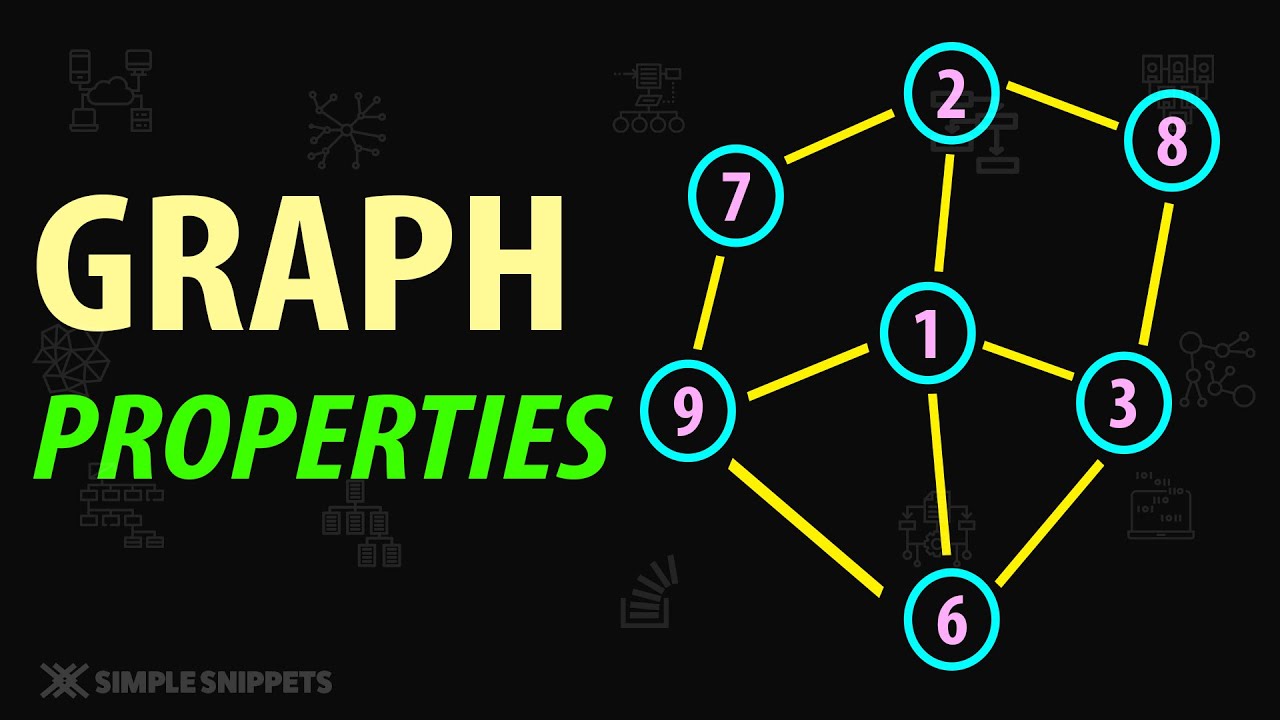
A graph is a non linear data structure consisting of nodes & edges connected in a way to form a network.
In this video we will study some properties of graphs -
Graph Mathematical representation -
A graph is a set of pair - (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices.
In the above graph,
V = {a, b, c, d, e, f}
E = {ab, ac, bd, bc, be, cf, de, ef}
Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.
Self-Loop − Is an edge that connects a vertex to itself. A simple graph contains no loops.
Multi Edge − two or more edges that are connecting to the same two vertices.
Simple Graph − Graphs without loops or parallel edges are called simple graphs.
The degree of a node − The degree of a node is the no of edges incident/attached on it.
Path − A path can be defined as the sequence of nodes that are followed in order to reach some terminal node E from the initial node A.
Simple Path − A path is a Simple path if no vertices(and thus edges) are not repeated
Cycle − A cycle can be defined as the path which has no repeated edges or vertices except the first and last vertices.
---------------------------------------------------------------------------------------------
Graph Theory -
Graph Full C++ Code Implementation -
---------------------------------------------------------------------------------------------
Support Simple Snippets by Donations -
---------------------------------------------------------------------------------------------
Timecodes -
00:00 Introduction & Recap
00:40 Graph representation
02:28 Graph Properties
---------------------------------------------------------------------------------------------
Simple Snippets Official Website -
Simple Snippets on Facebook -
Simple Snippets on Instagram -
Simple Snippets on Twitter -
Simple Snippets Google Plus Page -
Simple Snippets email ID -

#graph #graphds #datastructures

[shimwaben]

From East really appreciate your efforts bro 🤜🤛...I'm in love with this series ...it teaches me a lot in my self teaching Software development journey✌✌✌...God bless you 🙏🙏🙏

[sohailirfan]

Please upload all the topics of c++ Data structure and algorithms topic wise with their example as usual you do.
Thank you.
Your videos always helps me in programming.

[alijodat]

Yr work is amazing but i have a suggestion for you. Please arrange yr playlist in such a way that it would only have a particular topic in sequence. Although, you have videos covering all subtopics of a particular topic on yr channel but all of them scattered cuz they are not added to the playlist of that particular topic due to which videos are missed by viewers.

[bangunhapsoroofficial]

Creative and you make this simple.. Great...

[pankajsinghchamyal]

Please make vedio a little faster it is really helping me for my placement preparation .

[bdvw]

Hey Tanmay, I don't mean to be rude but how have you been? Is there a reason why the videos are so delayed? :)