filmov
tv
Quantum field theory, Lecture 2

Показать описание
This winter semester (2016-2017) I am giving a course on quantum field theory. This course is intended for theorists with familiarity with advanced quantum mechanics and statistical physics. The main objective is introduce the building blocks of quantum electrodynamics.
Here in Lecture 2 I discuss classical field theory and the least-action principle.
Here in Lecture 2 I discuss classical field theory and the least-action principle.
Quantum Field Theory Lecture - 2
Quantum field theory, Lecture 2
Quantum Field Theory II - Lecture 2
Advanced quantum field theory, Lecture 2
Dynamics of 2+1-dimensional Quantum Field Theory (Lecture - 02) by Nathan Seiberg
Quantum Field Theory Lecture 2: Klein Paradox (Transmission/Reflection from Potential Barrier)
Quantum Field Theory I - Lecture 2
Quantum Field Theory (HEP-QFT) Lecture 2 - Gauge Theory Lagrangian 2
Dirac Equation | Part 1 | Relativistic Quantum Mechanics #diracequation #physics #eduhubphysics
What 2 Semesters Of Quantum Field Theory Will Cover
Quantum Field Theory - Lecture 2: Functional Integrals 2 - Interacting Scalar Field-Feynman Diagrams
Kasia Rejzner - Renormalization in perturbative algebraic quantum field theory, Lecture 2
Quantum Field Theory 1b - Creation and Destruction II
2021 Bootstrap School - Edward Witten: Entanglement in Quantum Field Theory, Lecture 2
Quantum Field Theories in 2+1 Dimensions - Lecture 2
Quantum Field Theory 2b - Field Quantization II
Quantum Field Theory Explained in 2 Minutes
I Have to Give A Lecture On Quantum Field Theory
QFT: What is the universe really made of? Quantum Field Theory visualized
Quantum Field Theories in 2+1 Dimensions - Lecture 1
Dynamics of Quantum Fields in Three and Four Dimensions - Lecture 2
Ed Witten’s Quantum Field Theory: More Than Just Math
Lecture 3: Why Quantum Field Theory
Lecture 2: Symmetries and Conservation Laws
Комментарии
 1:03:43
1:03:43
 1:24:28
1:24:28
 2:20:41
2:20:41
 1:24:57
1:24:57
 1:34:41
1:34:41
 0:59:22
0:59:22
 1:21:12
1:21:12
 1:32:24
1:32:24
 1:34:18
1:34:18
 0:08:44
0:08:44
 1:28:09
1:28:09
 1:01:10
1:01:10
 0:16:23
0:16:23
 1:31:58
1:31:58
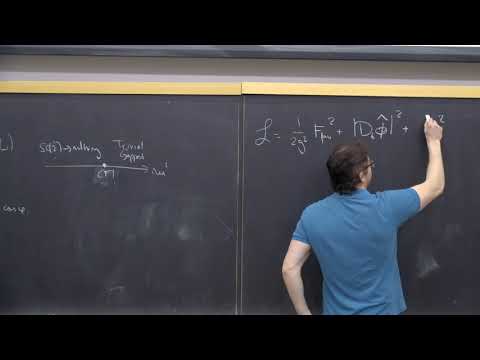 1:29:01
1:29:01
 0:09:56
0:09:56
 0:02:02
0:02:02
 0:03:56
0:03:56
 0:14:57
0:14:57
 1:45:49
1:45:49
 1:08:16
1:08:16
 0:00:40
0:00:40
 1:14:54
1:14:54
 1:21:32
1:21:32