SMUD seminar: Quantitative measure equivalence by Romain Tessera

Quantitative measure equivalence by Romain Tessera, University of Paris

Date: September 16, 2020

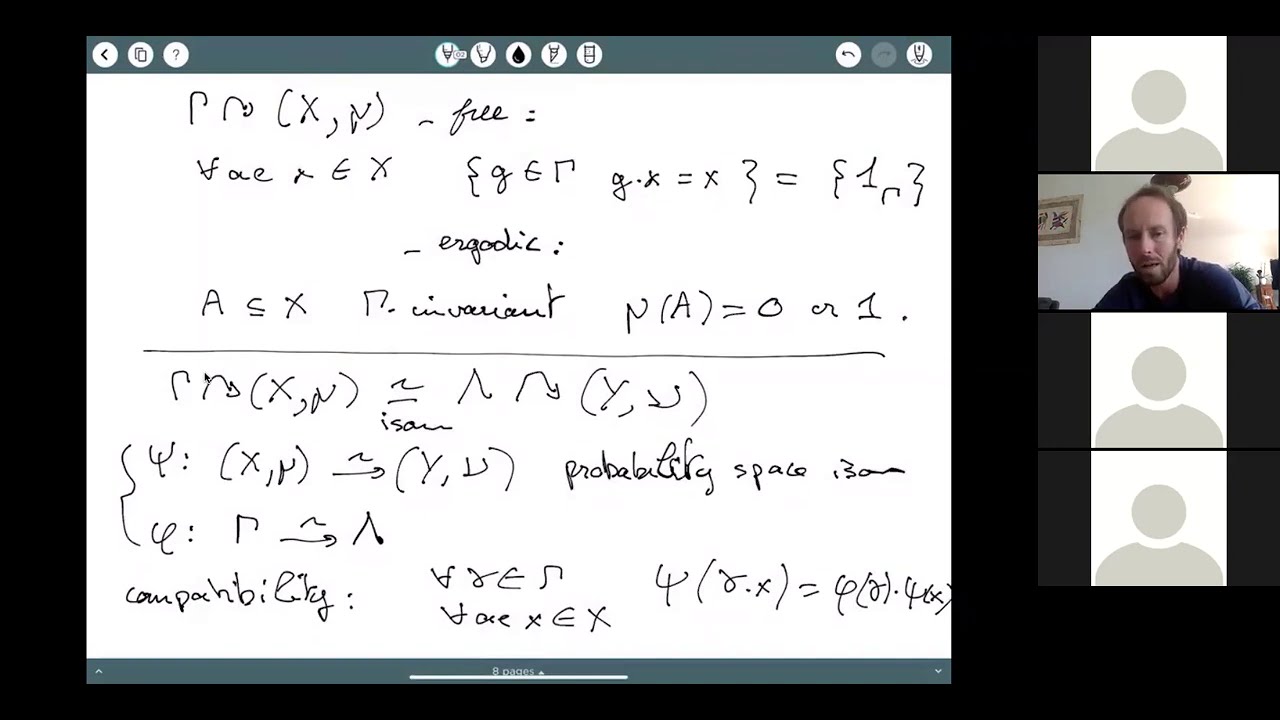
abstract: Measure equivalence is an equivalence relation between countable
groups that has been introduced by Gromov.
A fundamental instance are lattices in a same locally compact group.
According to a famous result of Orstein Weiss, all countable amenable
groups are measure equivalent, meaning that geometry is completely rubbed
out by this equivalence relation. Recently some more restrictive notions
have been introduced such as L^p-measure equivalence, where the associated
cocycles are assumed to be L^p-integrable. By contrast, a lot of
surprising rigidity results have been proved: for instance Bowen has shown
that the volume growth is invariant under L^1-measure equivalence, and
Austin proved that nilpotent groups that are L^1-measure equivalent have
bi-Lipschitz asymptotic cones. In this work we extend this study by trying
to understand more systematically how the geometry survives through measure
equivalence when an integrability condition is imposed. Our results go in
two directions: we prove rigidity results, culminating for amenable groups
with a general monotonicity result for the isoperimetric profile, and
flexibility results showing that in many instances, the previous result is
close to being optimal. We also prove a rigidity result for hyperbolic
groups, showing the optimality of a result of Shalom for lattices in
SO(n,1).