filmov
tv
How to solve a sudoku using 'The law of Symmetry' ?
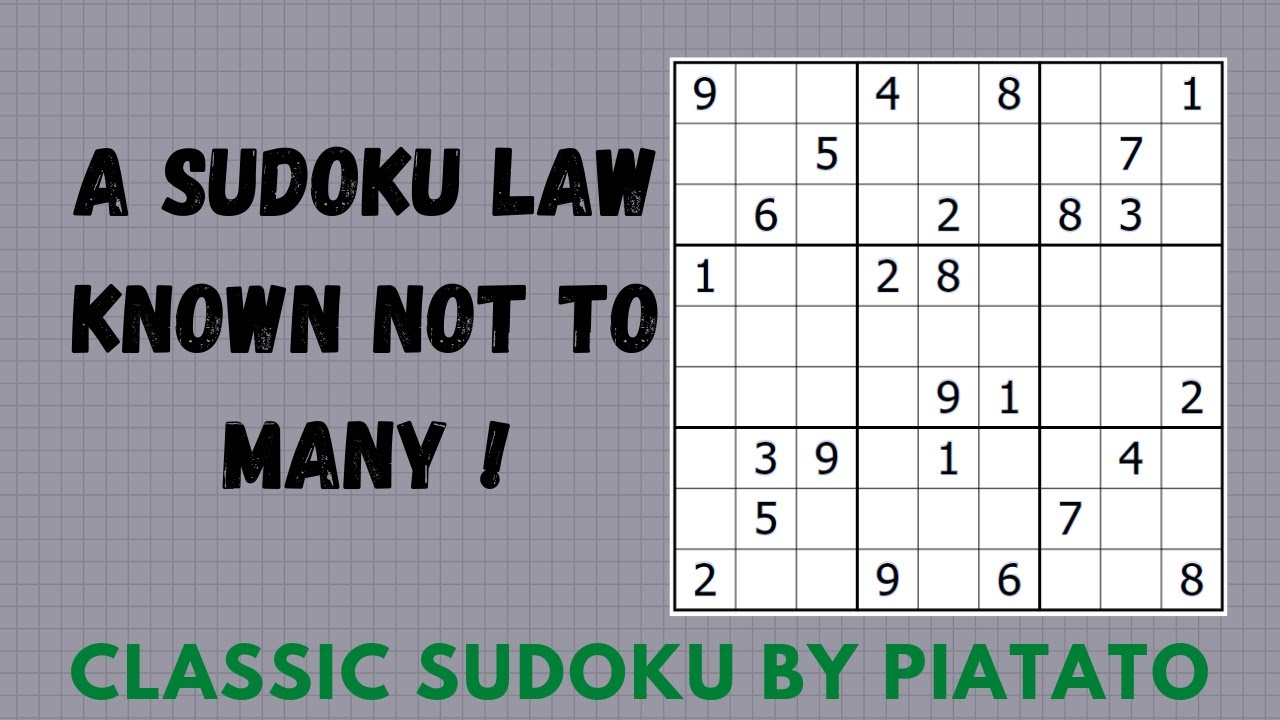
Показать описание
Piatato has carved out an absolutely mindboggling classic with a trick known only to a few in the sudoku world. So what are you waiting for ?
Try it out and check out the video !
Please subscribe to the channel if you love the work we are doing and want to support us !
Rules :
Place a digit from 1 to 9 in each empty cell so that each digit appears exactly once in each row, column and 3x3 box. Classic Sudoku rules apply.
Hello Everyone ! Welcome to this Youtube channel :
"Unshackling Sudokus & Puzzles "
#puzzles #sudokus #brainteasers # Classic # Piatato
I am Kishore Kumar Sridharan and I have been part of the team representing India in the World Sudoku Championship each year since 2015. I have also won the Classic Sudoku Master Event held during the Indian Sudoku Championship for a streak of 4 successive times. Solving sudokus and puzzles is my passion.
Try it out and check out the video !
Please subscribe to the channel if you love the work we are doing and want to support us !
Rules :
Place a digit from 1 to 9 in each empty cell so that each digit appears exactly once in each row, column and 3x3 box. Classic Sudoku rules apply.
Hello Everyone ! Welcome to this Youtube channel :
"Unshackling Sudokus & Puzzles "
#puzzles #sudokus #brainteasers # Classic # Piatato
I am Kishore Kumar Sridharan and I have been part of the team representing India in the World Sudoku Championship each year since 2015. I have also won the Classic Sudoku Master Event held during the Indian Sudoku Championship for a streak of 4 successive times. Solving sudokus and puzzles is my passion.
How to Solve a Sudoku Game
How To Do Hard Sudokus In 10 Minutes
How to Play Sudoku for Absolute Beginners
Tutorial #40 A must know technique. NOT a puzzle.
A Sudoku Secret to Blow Your Mind - Numberphile
Y-wing (XY Wing) - an Advanced Sudoku technique
How to play Sudoku
X-Wings and the Rectangle Rule for Solving Medium to Hard Sudoku Puzzles
Sudoku solution – The Guardian 7 January 2025 Medium level
How to play Sudoku in 30 seconds #sudoku #shorts
Top Nine Most Often Used Strategies for Solving Expert Sudoku Puzzles
How to Solve Sudoku Puzzles - Sudoku Beginner Tutorial #1
How to Solve Sudoku with This Easy Trick! #shorts
How to Solve Easy Sudoku Puzzles
Sudoku Secrets No. 2: The X-Wing #shorts
how to play Sudoku #puzzle #sudoku #brain #practice #enjoy #mindset
Making a Hard Sudoku really easy
The Best Sudoku Tip? Use Snyder Notation #shorts
Sudoku 'expert' level tricks. Sudoku expert level. How to solve sudoku expert level #puzzl...
Improve At Sudoku: What To Do When You Get Stuck
Episode #1: How to Solve an Easy Sudoku Puzzle - Follow Along
Techniques for Hard Sudoku
How to Solve Medium Sudoku Puzzles: Sudoku Intermediate Tutorial #1
Look How to Solve Sudoku
Комментарии
 0:02:57
0:02:57
 0:12:07
0:12:07
 0:08:00
0:08:00
 0:13:41
0:13:41
 0:06:08
0:06:08
 0:01:19
0:01:19
 0:01:14
0:01:14
 0:04:28
0:04:28
 0:11:43
0:11:43
 0:00:30
0:00:30
 0:04:28
0:04:28
 0:07:54
0:07:54
 0:00:15
0:00:15
 0:10:38
0:10:38
 0:00:59
0:00:59
 0:00:15
0:00:15
 0:06:47
0:06:47
 0:00:58
0:00:58
 0:12:12
0:12:12
 0:16:23
0:16:23
 0:27:05
0:27:05
 0:17:59
0:17:59
 0:10:34
0:10:34
 0:00:30
0:00:30