Converging-Diverging Nozzle Pressure Delineations

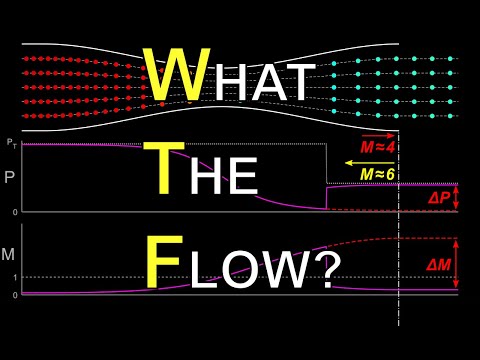
In my converging-diverging (CD) nozzle video (link below), we saw that there were seven different flow conditions in a nozzle. If know what exit-to-reservoir pressure ratio our engine is operating at (see notes below), then we can define what condition our nozzle is operating at based on three pre-computed pressure ratios:

1) Choked Isentropic Subsonic
2) Normal Shock at Nozzle Exit
3) Choked Isentropic Supersonic

In this video, we will compute the pressure ratios needed to obtain the three states listed above for a given nozzle area ratio (Ae/At).

===== NOTES =====
→ In this video, we can say that At = A* for each case because the flow is choked, and we do have sonic flow at the throat.

→ We generally know the exit-to-reservoir pressure ratio that our engine is operating at. For instance, if we are analyzing the Space Shuttle Main Engine (RS-25) on the launchpad, then we know the exit pressure is approximately 101.325 kPa. We also know from the engine's specifications that the reservoir (or chamber) pressure is approximately 20.64 MPa. Dividing the two appropriately gives the pressure ratio we are looking for.

===== RELEVANT LINKS=====
→ Blog Post - Converging-Diverging Nozzle Pressure Delineations

→ Solving the Area-Mach Number Relation

→ CD Nozzle MATLAB Code - GitHub

→ Compressible Flow Relations Code - GitHub

===== RELEVANT VIDEOS =====
→ Explained: Converging Diverging Nozzle

→ Area-Mach Number Relation [CPG]

→ Normal Shock Relations

→ Stagnation Relations

===== REFERENCES =====
► Modern Compressible Flow, Anderson
► Gas Dynamics, Volume 1, Zucrow and Hoffman
► Elements of Gasdynamics, Liepmann and Roshko

[MichaelMeUp]

GOd Bless you, you just saved me from getting destroyed at in fluids final

[junuhunuproductions]

7:42 I guess when rockets liftoff, the Normal Shock is not inside the nozzle, but the state is over-expanded, but as it goes into space, it becomes under-expanded(whilst passing the point where the efficiency is the greatest)

[dipanjandey]

Great vedio.. Me= f(area ratio, gamma), can you tell me the exact function?

[himoukooora]

red couler in tabble its bad plz change your couller annd you are great prof

[riseofzen]

This has been incredibly helpful, thanks a lot!
My lectures mentioned the different pressure ratios that results in the different flow conditions but never went over how to calculate them

[beachboardfan]

...need yourself a bigger whiteboard, and a patreon account.

[abdullahal-asmari]

One thing I dont get is how people relate the stagnation pressure before the shock to the static pressure AFTER the shock? the flow over a normal shock is adiabatic but the stagnation pressure after the shock is lower than the stagnation pressure before the shock so how do people find the pressure after the shock by using the stagnation pressure before the shock? it makes no sense and its driving me crazy.

[danielwalker]

Yours are some of the very best engineering education videos going. The way you handle the various cases is so clear. Every now and then, I get called upon to cover for a colleague and teach this material. I normally love equations, but I have always found these compressible flow eqns a pig. I teach the classes these days to solve problems using tables (which incidentally I churn out with Matlab and which I will happily share with anyone who's a use for them). Tables and interpolation is the way I was taught in the 1980s, using Howatson, Lund and Todd's Engineering Tables & Data (with gamma=1.4, of course!) and a text book by Massey. The (simple) codes I've written employ interpolation on a table rather than iterative root finding. I am definitely going to refer our students to your videos on this subject. Thank you.

[manelsouguir]

M exit is not equal to M1 because we have normal sock at the exit. Can you tell me please which relation have you used to calculate M exit ? I think we cannot use the normal sock relation P2/P1 ( as you have said at 6.51, because it is function of M1 isentropic), we cannot also use the isentropic relation of pressure because we have a sock . I guess we must use the relation A/A* .

[shemafonso]

Nicely explained
I hv a doubt, Say I'm designing a cd nozzles where the inlet pressure (combustion zone) is 5 bar (and of course velocity will not be zero thr). So can i take that 5 bar as stagnation pressure or do i need to find stagnation pressure?

[NitziPitzi]

Hey Josh! How did you know that the normal shock is at the exit in the first place?

[Hunter-]

Why are the turbine nozzles made divergent after the throat?

[MsDehane]

first i want to tell you that you are amazing
also i want ask you if you can make video where you explain the characteristic method for design a CD nozzle
think you very much Sir