Sparse Gaussian Processes on Matrix Lie Groups: A Unified Framework for Optimizing Continuous-Time T

preview_player
Показать описание
ICRA 2018 Spotlight Video
Interactive Session Thu AM Pod U.4
Authors: Dong, Jing; Mukadam, Mustafa; Boots, Byron; Dellaert, Frank
Title: Sparse Gaussian Processes on Matrix Lie Groups: A Unified Framework for Optimizing Continuous-Time Trajectories

Abstract:
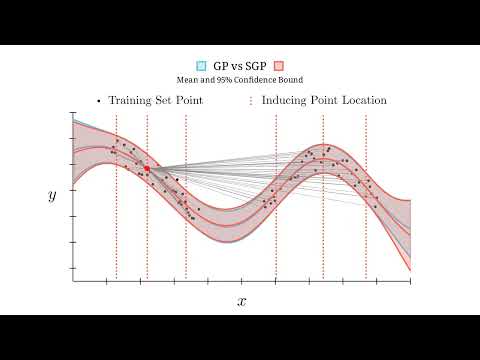
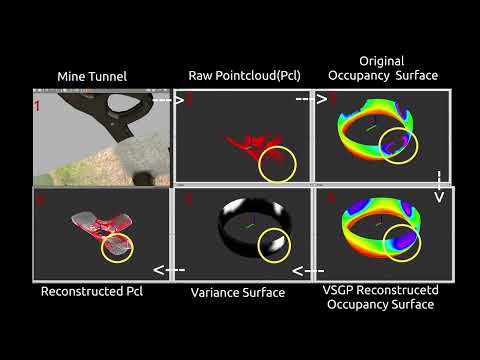
Continuous-time trajectories are useful for reasoning about robot motion in a wide range of tasks. Sparse Gaussian processes (GPs) can be used as a non-parametric representation for trajectory distributions that enables fast trajectory optimization by sparse GP regression. However, most previous approaches that utilize sparse GPs for trajectory optimization are limited by the fact that the robot state is represented in vector space. In this paper, we first extend previous works to consider the state on general matrix Lie groups by applying a constant-velocity prior and defining locally linear GPs. Next, we discuss how sparse GPs on Lie groups provide a unified continuous-time framework for trajectory optimization for solving a number of robotics problems including state estimation and motion planning. Finally, we demonstrate and evaluate our approach on several different estimation and motion planning tasks with both synthetic and real-world experiments.
  1. ICRA 2018
  2. SLAM
  3. Probability and Statistical Methods
  4. Motion and Path Planning
Рекомендации по теме
Sparse Gaussian Processes 0:02:34

Sparse Gaussian Processes on Matrix Lie Groups: A Unified Framework for Optimizing Continuous-Time T

Multi-Robot Informative Path 0:07:00

Multi-Robot Informative Path Planning from Regression with Sparse Gaussian Processes

Sparse Orthogonally-Decoupled Gaussian 0:01:13

Sparse Orthogonally-Decoupled Gaussian Process Regression

Illustration of sparse 0:00:31

Illustration of sparse Gaussian processes

James Hensman: Sparse 1:02:48

James Hensman: Sparse Gaussian Processes

Gaussian Processes 0:23:47

Gaussian Processes

Sparse Gaussian Process 1:30:23

Sparse Gaussian Process Approximations, Richard Turner

SOLAR-GP: Sparse Online 0:10:00

SOLAR-GP: Sparse Online Locally Adaptive Regression Using Gaussian Processes for Robot Learning

12.3 Variational Zero-Inflated 0:16:57

12.3 Variational Zero-Inflated Gaussian Process With Sparse Kernels

Light-Weight Pointcloud Representation 0:02:46

Light-Weight Pointcloud Representation with Sparse Gaussian Process

Illustration of streaming 0:00:15

Illustration of streaming sparse Gaussian processes

Predictive Uncertainty Estimation 0:05:01

Predictive Uncertainty Estimation of Neural Networks with Sparse Gaussian Processes

Scalable Log Determinants 0:03:15

Scalable Log Determinants for Gaussian Process Kernel Learning - NIPS 2017

James Hensman, Alan 1:48:03

James Hensman, Alan Saul: Sparse Gaussian Processes and with non-Gaussian Likelihoods

ML Tutorial: Gaussian 1:53:32

ML Tutorial: Gaussian Processes (Richard Turner)

Recent Advances in 1:16:44

Recent Advances in Gaussian processes

Multimodal Policy Search 0:01:14

Multimodal Policy Search using Overlapping Mixtures of Sparse Gaussian Process Prior

Lecture 7.3 - 1:02:16

Lecture 7.3 - Gaussian Processes

Dual parameterization of 0:13:52

Dual parameterization of sparse variational Gaussian processes

Light-weight Pointcloud Representation 0:02:59

Light-weight Pointcloud Representation using Sparse Gaussian Process #ICRA23

Paper Club with 0:41:15

Paper Club with Ben - Matérn Gaussian Processes on Graphs

GPSS workshop: A 0:57:15

GPSS workshop: A Unifying Framework for Sparse GP Approximation using Power EP, Richard Turner

Using Sparse Gaussian 0:00:44

Using Sparse Gaussian Processes for Predicting Robust Inertial Confinement Fusion Implosion Yields

Approximate Real-Time Optimal 0:04:22

Approximate Real-Time Optimal Control Based on Sparse Gaussian Process Models