filmov
tv
Q does not has least upper bound Property, R has least upper bound property. Real Analysis I, Lec-08

Показать описание
**Note. If a set has least upper bound property we say it is complete so R is completer an Q is not complete.
*****pdf notes of these video lectures can be down loaded from our following face book group.
**************************************************************************************
To watch all videos of the playlist "Real Analysis I" visit the following:
************************************************************************************
For more educational videos of maths visit our channel
*********************************************************************************
In this part of lecture series course "Real Analysis I" Course of BS mathematics 5th Semester, we shall cover the following topics.
Real Number System
Ordered sets, fields, the field of real numbers
Completeness property of R
The extended real number system
Euclidean spaces
Finite, countable and uncountable sets
Sequences and Series
Sequences, subsequences, convergent sequences, Cauchy sequences
Monotone and bounded sequences, Bolzano Weierstrass theorem
Series, series of non-negative terms
Partial sums, the root and ratio tests, integral test, comparison test
Absolute and conditional convergence
Limit and Continuity
The limit of a function
Continuous functions
Types of discontinuity
Uniform continuity
Monotone functions
Differentiation
The derivative of a function
Mean value theorems, the continuity of derivatives
Taylor’s theorem
Functions of Several Variables
Partial derivatives and differentiability, derivatives and differentials of composite functions
Change in the order of partial derivative, implicit functions, inverse functions, Jacobians
Maxima and minima
Recommended Books
1. W. Rudin, Principles of Mathematical Analysis, 3rd edition, (McGraw Hill, 1976)
2. R. G. Bartle, Introduction to Real Analysis, 3rd edition, (John Wiley and Sons, 2000)
***********************************************************************************************
We shall be thankful to all those, who will comment and message us on our channels whatsapp number (092)03154414993.
*****pdf notes of these video lectures can be down loaded from our following face book group.
**************************************************************************************
To watch all videos of the playlist "Real Analysis I" visit the following:
************************************************************************************
For more educational videos of maths visit our channel
*********************************************************************************
In this part of lecture series course "Real Analysis I" Course of BS mathematics 5th Semester, we shall cover the following topics.
Real Number System
Ordered sets, fields, the field of real numbers
Completeness property of R
The extended real number system
Euclidean spaces
Finite, countable and uncountable sets
Sequences and Series
Sequences, subsequences, convergent sequences, Cauchy sequences
Monotone and bounded sequences, Bolzano Weierstrass theorem
Series, series of non-negative terms
Partial sums, the root and ratio tests, integral test, comparison test
Absolute and conditional convergence
Limit and Continuity
The limit of a function
Continuous functions
Types of discontinuity
Uniform continuity
Monotone functions
Differentiation
The derivative of a function
Mean value theorems, the continuity of derivatives
Taylor’s theorem
Functions of Several Variables
Partial derivatives and differentiability, derivatives and differentials of composite functions
Change in the order of partial derivative, implicit functions, inverse functions, Jacobians
Maxima and minima
Recommended Books
1. W. Rudin, Principles of Mathematical Analysis, 3rd edition, (McGraw Hill, 1976)
2. R. G. Bartle, Introduction to Real Analysis, 3rd edition, (John Wiley and Sons, 2000)
***********************************************************************************************
We shall be thankful to all those, who will comment and message us on our channels whatsapp number (092)03154414993.
Комментарии
 0:05:39
0:05:39
 0:00:27
0:00:27
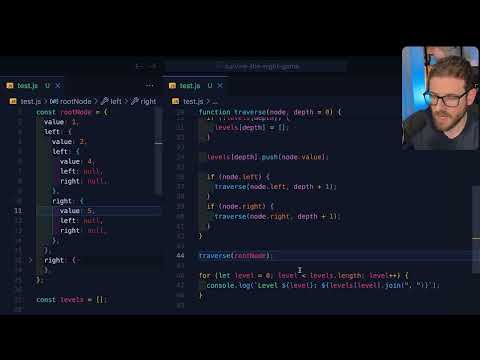 0:10:01
0:10:01
 0:00:10
0:00:10
 0:07:42
0:07:42
 0:03:09
0:03:09
 0:06:24
0:06:24
 0:00:23
0:00:23
 0:04:01
0:04:01
 0:13:36
0:13:36
 0:14:40
0:14:40
 0:00:58
0:00:58
 0:00:26
0:00:26
 0:02:36
0:02:36
 0:00:24
0:00:24
 0:00:57
0:00:57
 0:05:40
0:05:40
 0:02:47
0:02:47
 1:33:46
1:33:46
 0:00:11
0:00:11
 0:09:42
0:09:42
 0:08:02
0:08:02
 0:00:27
0:00:27
 0:00:59
0:00:59