filmov
tv
SOA Exam P Question 145 | Conditional Joint Variance

Показать описание
New dental and medical plan options will be offered to state employees next year. An
actuary uses the following density function to model the joint distribution of the
proportion X of state employees who will choose Dental Option 1 and the proportion Y
who will choose Medical Option 1 under the new plan options:
Calculate Var (Y | X = 0.75).
(A) 0.000
(B) 0.061
(C) 0.076
(D) 0.083
(E) 0.141
You can find the link to the questions below:
The link to the answers below:
Check out my other channel Rumi's Life:
actuary uses the following density function to model the joint distribution of the
proportion X of state employees who will choose Dental Option 1 and the proportion Y
who will choose Medical Option 1 under the new plan options:
Calculate Var (Y | X = 0.75).
(A) 0.000
(B) 0.061
(C) 0.076
(D) 0.083
(E) 0.141
You can find the link to the questions below:
The link to the answers below:
Check out my other channel Rumi's Life:
SOA Exam P Question 145 | Conditional Joint Variance
Actuarial SOA Exam P Sample Question 145 (once 196) Solution
SOA/FM SAMPLE QUESTION #145
Formerly SOA P Sample Question 145 (This Question has now been deleted by SOA)
Actuarial SOA Exam P Sample Question 146 (once 197) Solution
SOA Exam P Question 144 | Multivariate Probability
Actuarial SOA Exam P Sample Question 226 (once 288) Solution
Actuarial SOA Exam P Sample Question 56 (once 62) Solution
SOA Exam P Question 186 | Two step Normal Distribution with Continuity Correction
Actuarial SOA Exam P Sample Question 98 (once 142) Solution
Actuarial SOA Exam P Sample Question 105 (once 151) Solution
Actuarial SOA Exam P Sample Question 102 ( once 148) Solution
Actuarial SOA Exam P Sample Question 144 (once 195) Solution
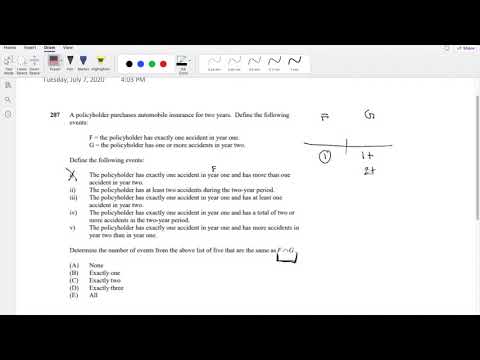
SOA Exam P Question 207 | Intersection of Events
SOA Exam P Question 146 | Triple Venn Diagram
Actuarial SOA Exam P Sample Question 129 (once178) Solution
Actuarial SOA Exam P Sample Question 109 (once 155)
Actuarial SOA Exam P Sample Question 114 (160 once) Solution
Exam P #62 | SOA Sample Questions
Actuarial SOA Exam P Sample Question 243 (once 310) Solution
Formerly SOA P Sample Question 138 (This Question has now been deleted by SOA)
Actuarial SOA Exam P Sample Question 318 Solution
SOA Exam P Question 150 | Percentile and Exponential Distribution
Actuarial SOA Exam P Sample Question 162 (once 216) Solution
Комментарии
 0:05:34
0:05:34
 0:08:45
0:08:45
 0:05:40
0:05:40
 0:07:48
0:07:48
 0:07:31
0:07:31
 0:01:39
0:01:39
 0:08:16
0:08:16
 0:04:58
0:04:58
 0:05:42
0:05:42
 0:03:21
0:03:21
 0:07:04
0:07:04
 0:04:51
0:04:51
 0:02:24
0:02:24
 0:02:17
0:02:17
 0:03:05
0:03:05
 0:02:27
0:02:27
 0:07:32
0:07:32
 0:01:33
0:01:33
 0:12:21
0:12:21
 0:03:35
0:03:35
 0:03:40
0:03:40
 0:03:34
0:03:34
 0:03:20
0:03:20
 0:07:58
0:07:58