filmov
tv
Calculating sin(π/5) Using a Regular Pentagon

Показать описание
The exact value of sin(𝜋/5) is (sqrt(10–2sqrt(5))/4. 😎
We can find it using a regular pentagon, some similar triangles and the Pythagorean theorem...
Written Article:
Interesting article about Gauss-Wantzel Theorem:
We can find it using a regular pentagon, some similar triangles and the Pythagorean theorem...
Written Article:
Interesting article about Gauss-Wantzel Theorem:
Calculating sin(π/5) Using a Regular Pentagon
The Exact Value of sin(π/5) is Here in the Pentagon
What is This EXACTLY ? [Calculating the Exact Value of Sin(Pi/5)]
Find the exact value of sin pi/5 and cos pi/5 , related to golden ratio
Learn how to find the sine of 5 pi over 4 without a calculator
The exact value of sin(π/5)
When mathematicians get bored (ep1)
Prépa-Les complexes-Racines 5-ième - cos(2pi/5) et sin(pi/5)-Colle
Advanced Higher Maths PRELIM Ultimate Exam Revision Guide | Everything in 2 Hours!
How To Use a Calculator To Calculate The Exact Value of Cos Pi over 3 | tan(pi/3)
Compute sin(pi) by Hand without a Calculator by using the Unit Circle
sin(pi/5)
Calcul de sin(pi/5) (CPGE 1ère année & L1)
Mastering Complex Numbers: Solving Sin(π/14)Sin(3π/14)Sin(5π/14) Using Euler's Formula
Solve | sin 30 degree | using calculator (Casio fx-991MS)
How To Find cos(pi/5), sin(pi/5) | MSM math
Sine Curve and the Unit Circle
And You Thought Trigonometry Was Pointless…
5 simple unsolvable equations
How to Find Exact Value of cos18 sin 18 or sin pi by 10 sin 36 cos pi by 10 and cos 36
How to calculate inverse sin in scientific calculator #scintific #calculator #studenthacks
Fix scientific calculator issue. change settings from radians to degree. values of sin, cos or tan
sin(pi/5) cos(pi/5) найти значение функции #maths #math #calculus #complexnumbers #reductionformula...
Trigonometric Values 0, π/2, π, 3π/2, 2π,⋅⋅⋅ at Lightning Speed
Комментарии
 0:03:50
0:03:50
 0:00:43
0:00:43
 0:05:34
0:05:34
 0:04:56
0:04:56
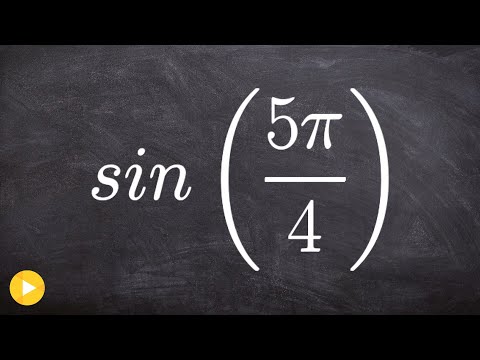 0:04:30
0:04:30
 0:09:41
0:09:41
 0:00:37
0:00:37
 0:09:34
0:09:34
 2:06:05
2:06:05
 0:00:24
0:00:24
 0:01:07
0:01:07
 0:06:03
0:06:03
 0:12:39
0:12:39
 0:06:26
0:06:26
 0:00:24
0:00:24
 0:07:22
0:07:22
 0:00:27
0:00:27
 0:01:00
0:01:00
 0:00:50
0:00:50
 0:21:38
0:21:38
 0:00:15
0:00:15
 0:01:27
0:01:27
 0:00:56
0:00:56
 0:06:06
0:06:06