filmov
tv
Bertrand's Ballot Theorem

Показать описание
Bertrand's Ballot Theorem
Sorry for the vertical video, this was originally posted on Tiktok!
Read more:
Corrections:
Sorry for the vertical video, this was originally posted on Tiktok!
Read more:
Corrections:
Bertrand's Ballot Theorem
Bertrand's ballot theorem
Joseph Bertrand Ballot Theorem
Bertrand's Ballot Theorem
Lecture 8.2: f. The ballot problem: 3. The solution — [Probability | Santosh S. Venkatesh]
Lecture 8.2: d. The ballot problem: 1. The setting — [Probability | Santosh S. Venkatesh]
08-06. Conditional expectation - Conditioning: the ballot problem.
Bertrand's Ballot Problem | Derangements | Combinatorics for ISI MStat & IIT JAM MS
Ballot problem
Bertrand's Paradox - Probability | WIRELESS PHILOSOPHY
Lecture 8.2: e. The ballot problem: 2. The wisdom of Lao Tzu — [Probability | Santosh S. Venkatesh]...
More on Bertrand's Paradox (with 3blue1brown) - Numberphile
On Virtual Pascal's Triangles: The Ballot Problem
BERTRAND'S POSTULATE MATHEMATICS ISI ,DSE ,JNU ,IGIDR ,CSIR NET ,NPTEL ,MIT ,IIT JAM ,UPSC ,M...
Challenging Problems in Probability: The Ballot Box
The Most Controversial Problem in Philosophy
Random Dictatorship and Gibbard's 1977 Theorem | Lê Nguyên Hoang
Bertrand's Box Paradox
Le jugement majoritaire | Démocratie 4
Richard Dawkins On What Happens When You Die
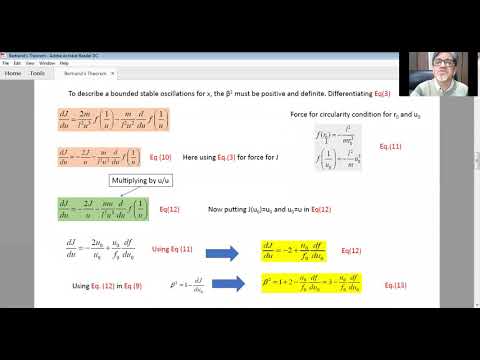
Bertrand's Theorem | Prof. Mihir J. Joshi, Department of Physics, Saurashtra University | Lec 0...
Why Democracy Is Mathematically Impossible
Bertrand Rémy: Bruhat-Tits theory of quasi-split groups
Bertrand Russell's Philosophy
Комментарии
 0:01:40
0:01:40
 0:01:29
0:01:29
 0:09:41
0:09:41
 0:24:04
0:24:04
 0:11:48
0:11:48
 0:10:39
0:10:39
 0:19:23
0:19:23
 1:59:45
1:59:45
 0:01:08
0:01:08
 0:07:44
0:07:44
 0:13:09
0:13:09
 0:23:38
0:23:38
 0:11:35
0:11:35
 0:07:19
0:07:19
 0:10:31
0:10:31
 0:10:19
0:10:19
 0:10:46
0:10:46
 0:03:53
0:03:53
 0:17:04
0:17:04
 0:00:55
0:00:55
 0:33:03
0:33:03
 0:23:34
0:23:34
 1:34:48
1:34:48
 0:17:35
0:17:35