Find X value from given right side area| Standard Normal Distribution Curve| Leaving Cert Maths |

Task:
In English the top 15% of students were awarded an A grade.

Find the least whole number mark that merited the award of an A grade in English

Given information:
The percentage results in an English exam for the class had a mean
mark of 72 with a standard deviation of 10. The results in both exams were normally
distributed.

The probability that a random variable Z is greater than certain z is given as 15% or 0.15.
This equals the area under the curve, to the right side of point z.
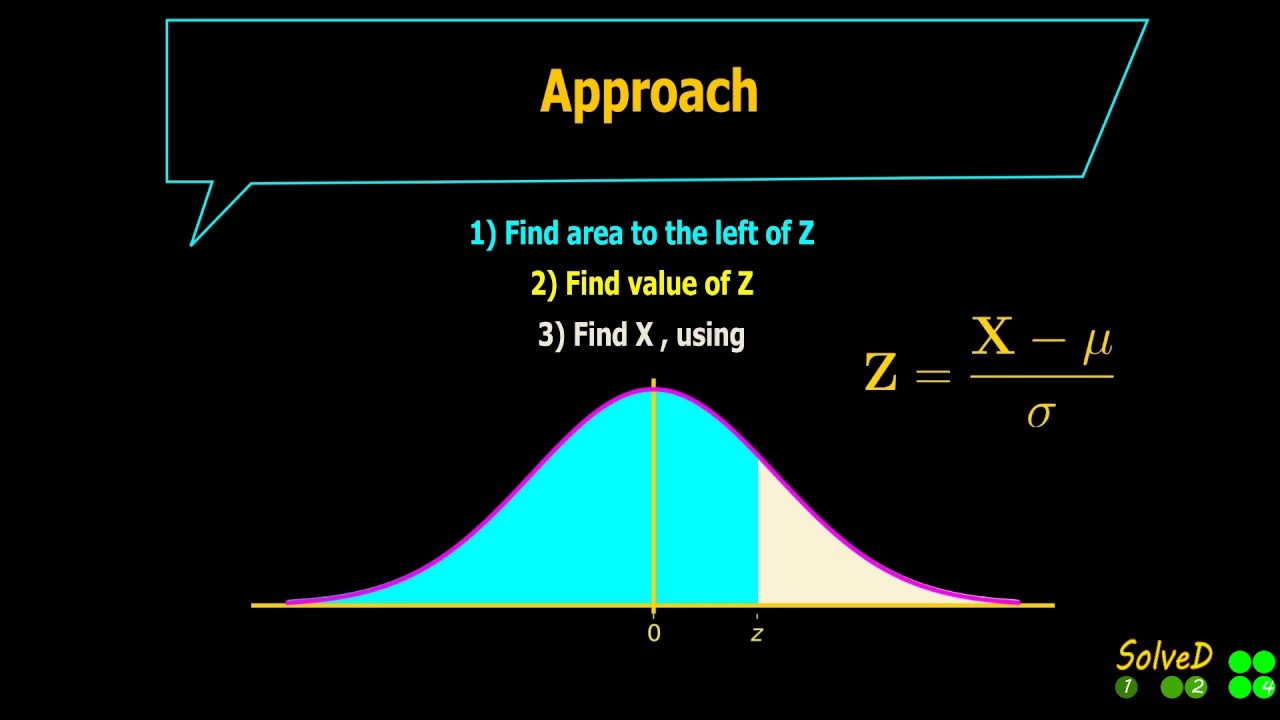
Using this the left area = 1- 0.15 = 0.85.
Now using this we can find the value of z. Using this value in the equation of transformation, we can find the corresponding X value.
***************************************************
Contents:
(1) Problem description
(2) Approach
(3) Solution
(4) Key points
***************************************************
Leaving Cert | HL| Exam | 2018 B | Q2(b)(ii) |
***************************************************
#LeavingCert#Maths
#SolveD124 | SolveD124