Simplifying Radicals Easy Way

Answers for the Practice section:

Hi, this is Demóclis Rocha from Learn Math With Me.
I am here to help you to boost your score in your math class. Improve your understanding and hopefully make learning math a lot less stressful.
So what we are going to talk about in this vídeo is an easy way to simplify radicals. An easy method.
Many times when teachers try to teach this they say “try to divide out perfect squares”, like you divide out 4, 9, 16, 25, 36,... you divide out perfect squares so you can simplify the radical. One problem with this method is sometimes students strugle trying to divide out perfect squares.
In this method what we are going to do is, first, a prime factorization tree. Because in this case we are dealing with a square root, you don’t see it, but there is a two understood here, we will look for pairs of the same prime fator once we have finished the prime factorization tree. If you are taking a cube root you look for three of the same prime number, if you are taking a forth root you look for 4 of the same prime number and so on.

Let’s start by breaking down the number, for instance, 80 equals 2 times 40. Now, 40 equals 2 times 20. Then, 20 equals 2 times 10. Finally, 10 equals 2 times 5.

We have a one pair of 2 here, so we write a two right here. There is another pair of 2 here, so we multiply by 2 here. Finally there is a 5 here left over. It remains underneath the radical, since it does not pair up. Notice that we used only the prime numbers in the ends ok the branches.
Since 2 times 2 equals 4, the result is 4 times the square root of 5 or just 4 square root of 5.
To check your answer you look at this number on the outside, you square it, the square of 4 is 16, then you multiply by the number on the inside 5. Well, 16 times 5 equals the original 80, so our answer is correct.
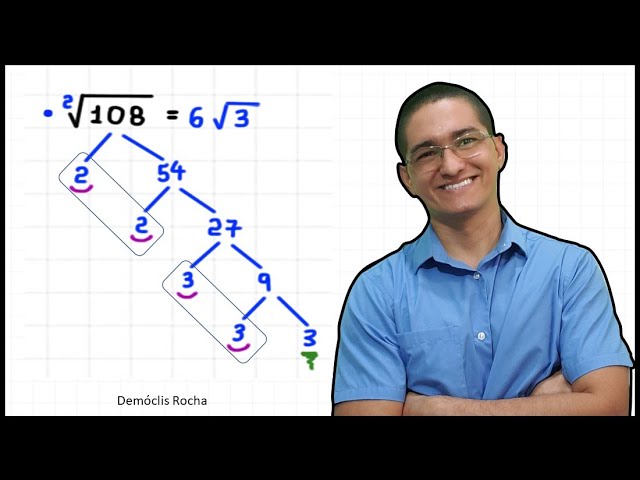
Now, let’s take a look at another example. The square root of 108. An even number ends with 0, 2, 4, 6 or 8. Since 108 ends in 8, it is an even number and it is divisible by 2. Notice that 108 equals 2 times 54. Now, 54 is also even, and 54 equals 2 times 27. Now, 27 is not even, but it is divisible by 3. You know that 3 times 9 equals 27. Finally, 9 equals to 3 times 3.
We have a pair of 2 here, I right a 2 here, times..., we have a pair of 3 here, so I right 3 here. But there is a 3 left over. So I write 3 underneath the radical.
Since 2 times 3 equals 6, our final answer is 6 square root of 3. If you want to check, notice that the square of 6 is 36, and 36 multiplied by what is on the inside, 36 times 3 equals 108, that is what we had in the begining.
Now we have a cube root. So when we finish the prime factorization tree, we look for 3 of the same prime number in the ends for the branches.
240 is even and it is 2 times 120. Now, 120 is also even and it is 2 times 60. The number 60 is equal to 2 times 30. Now, 30 equals to 2 times 15. Finally, 15 equals to 3 times 5.
Here we have 3 of the same prime number 2, so I write 2 here. The other prime numbers left don’t form a group of 3 of the same, so we are left with 2 times 3, that is 6, and 6 times 5 that is 30.
So our final answer is 2 cube root of 30.
Notice that the cube of 2 is 8 and 8 times what is on the inside is 8 times 30 that is equal to 240, that is what we had in the begining so our result is correct.
Practice makes perfect. If you want to keep practicing, you can simplify the square root of 48, the square root of 72 and the cube root of 96. I’ll leave a link to a vídeo with na explanation for these in the description.
If this vídeo somehow helped you, leave a comment with a smile face. I will be happy to see it.
That’s it for today, have a nice day. Bye.