filmov
tv
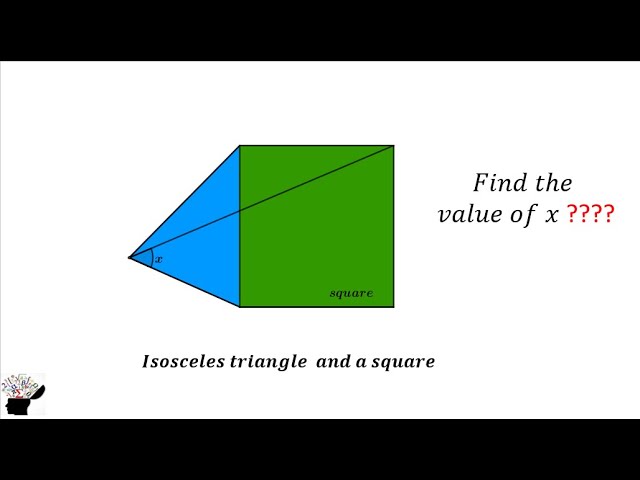
A square and an isosceles triangle. Could you find the value of x?
Показать описание
Geometry, Polynomial expressions, sum of squares, algebra, algebraic equations, substitution, Challenging Math Problems, polynomial equations, algebra challenge, algebraic identities, algebraic challenge.
A square and an isosceles triangle. Could you find the value of x?
Math in the Simpsons: Homer's theorem
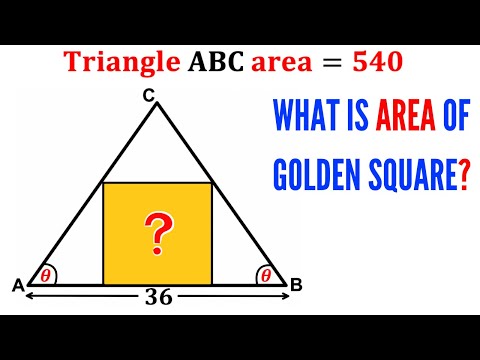
Olympiad Mathematics | Find area of the pink square | (Isosceles triangles) | #math #maths
Three square on an isosceles right triangle
Square games
Isosceles triangle inside square | Find the angle | Advanced math problems | Mathematics
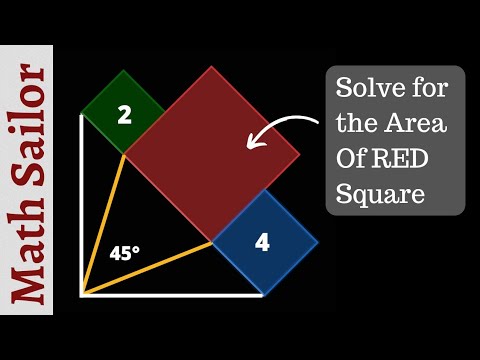
Math Olympiad | Can you find area of the Golden shaded square? | (Isosceles triangle) | #math #maths
Quadratic App: Find the Height of an Isosceles Triangle (Square Roots)
How to draw an equilateral triangle with side 4.5 cm
A square is inscribed in an isosceles right triangle so that the square and the triangle have one...
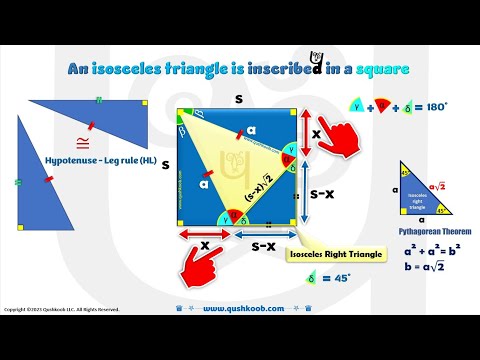
Isosceles triangle is inscribed in a square in two ways. A square inside an isosceles triangle #math
[The Simpsons] Sum of the Square Roots of Any Two Sides of an Isosceles Triangle see description
If the square of hypotenuse of an isosceles right triangle is 200 cm² . Find the length of bases.
7.A kite in the shape of a square with a diagonal 32cm and an isosceles triangles of base 8cm and si...
A square is inscribed in an isosceles right triangle so that the square and the triangle have one...
If the square of the hypotenuse of an isosceles right triangle is 98 what is the length of each side
A rectangle is inscribed in a square creation for isosceles right triangle.
Isosceles triangle inside square | Find the angle | Advanced math problems | Mathematics
YTPµ of the Day: The Square Root Of An Isosceles Triangle
Square Inscribed in a Right Triangle. Geometry video.
Area of an Irregular Shape - Square Minus Isosceles Triangle
The area of an isosceles triangle is 4 square unit. If the length of the third side is 2 unit, the
A square is inscribed in an isosceles right triangle so that the square and the triangle have one a
Properties of Isosceles Right Triangles : Solving Math Problems
Комментарии
 0:03:51
0:03:51
 0:08:41
0:08:41
 0:10:46
0:10:46
 0:14:39
0:14:39
 0:00:18
0:00:18
 0:05:26
0:05:26
 0:08:55
0:08:55
 0:03:51
0:03:51
 0:01:42
0:01:42
 0:06:00
0:06:00
 0:12:12
0:12:12
![[The Simpsons] Sum](https://i.ytimg.com/vi/JNLdTEJzjjE/hqdefault.jpg) 0:00:08
0:00:08
 0:02:05
0:02:05
 0:03:28
0:03:28
 0:04:06
0:04:06
 0:03:34
0:03:34
 0:04:37
0:04:37
 0:00:39
0:00:39
 0:00:09
0:00:09
 0:01:30
0:01:30
 0:02:29
0:02:29
 0:06:37
0:06:37
 0:17:00
0:17:00
 0:02:13
0:02:13