filmov
tv
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (32 of 92) Finite Potential Well Part 1

Показать описание
In this video I will explain the particle in a finite well instead of an infinite well. Which means the barriers does not have infinite height or energy. In quantum mechanics that means the particle can venture outside of the trapped region. For example if region 1 is the barrier on the left-side, region 3 is the barrier on the right-side, and region 2 is in the middle where the particle is located, and if the barrier is infinite in height that means it'll require an infinite amount of energy for the particle to cross the barrier into regions 1 and 3. However if the energy required to cross into regions 1and 3 is finite, then the particle can reside in region 1 or 3. (Part 1)
Next video in this series can be seen at:
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (1 of 92) The Wave Equation
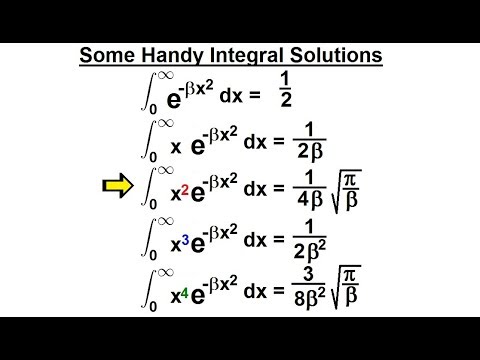
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (59 of 92) Some Handy Integral Solutions
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (69 of 92) Is this Possible???
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (54 of 92) The wave Function
Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (2 of 38) How are Photons Absorbed? 1
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (49 of 92) How Oscillators Increase Energy
Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (17 of 38) E=mc^2 and the Mass of Proton
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator
Light (lec -4) | class 10 | physics ch-1 (Raw lecture) | NODOUBT CLASSES JBP
Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (4 of 38) Absorber Thickness
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (42 of 92) k=? of a Diatomic Molecule
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (40 of 92) What is Reduced Mass?
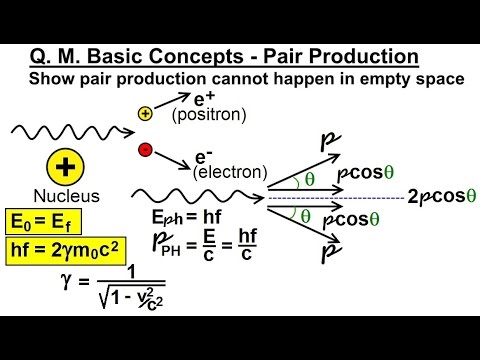
Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (1 of 38) What is Pair Production?
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (80 of 92) Transmission Coeff. Example
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (92 of 92) Modeling Polonium-212 Decay
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (32 of 92) Finite Potential Well Part 1
Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (5 of 38) Absorber Thickness: Example
Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (14 of 38) What is Gravitation Redshift? 1
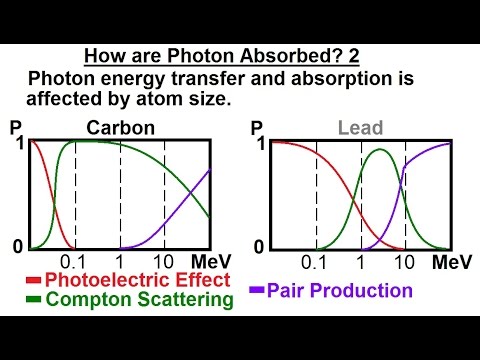
Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (3 of 38) How are Photons Absorbed? 2
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (81 of 92) Transmission Coeff., Original Eq
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (67 of 92) Finding R=? T=? Coefficients
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (13 of 92) Time & Position Dependencies ...
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (91 of 92) Modeling Polonium-212 Decay
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (53 of 92) The wave Equation
Комментарии
 0:07:41
0:07:41
 0:01:38
0:01:38
 0:02:40
0:02:40
 0:02:56
0:02:56
 0:07:03
0:07:03
 0:03:38
0:03:38
 0:01:53
0:01:53
 0:03:24
0:03:24
 0:55:05
0:55:05
 0:06:55
0:06:55
 0:04:59
0:04:59
 0:03:48
0:03:48
 0:07:19
0:07:19
 0:05:50
0:05:50
 0:05:40
0:05:40
 0:05:50
0:05:50
 0:06:22
0:06:22
 0:09:45
0:09:45
 0:04:34
0:04:34
 0:04:10
0:04:10
 0:08:23
0:08:23
 0:07:07
0:07:07
 0:07:05
0:07:05
 0:03:02
0:03:02