Order 2 Elements in Finite Group

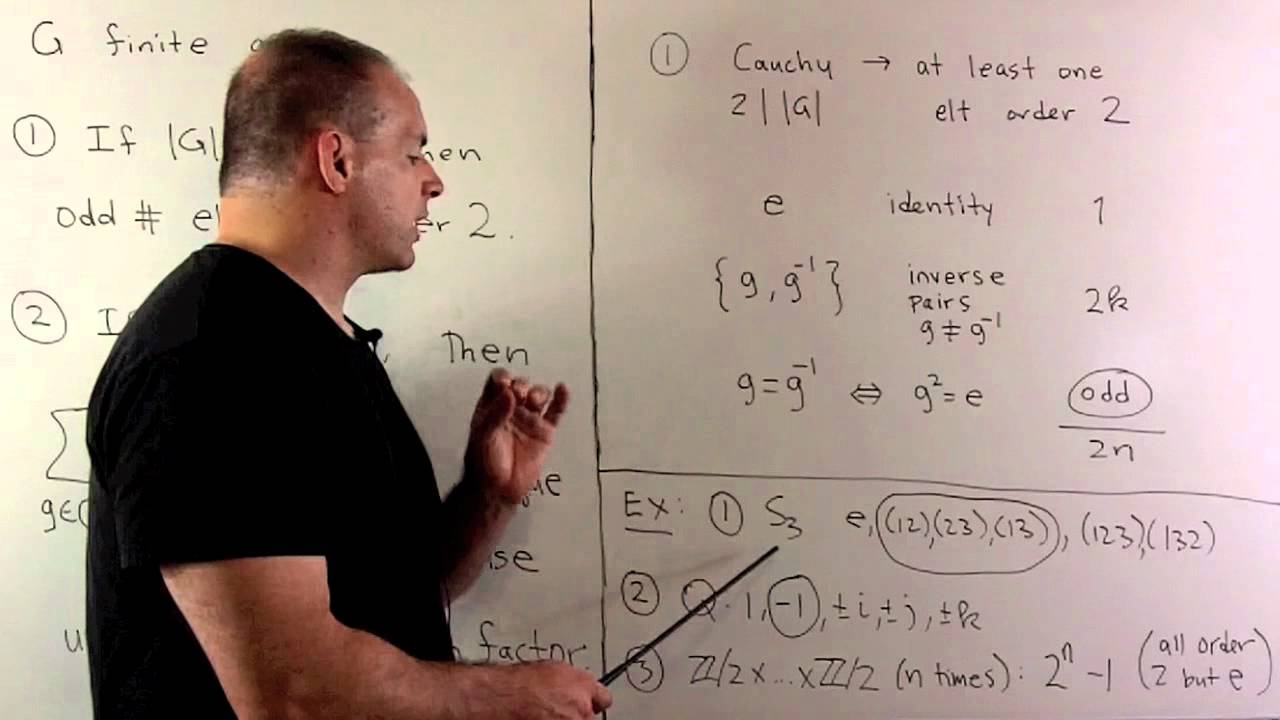
preview_player
Показать описание
Abstract Algebra: Let G be a finite group. (1) If |G| is even, show that G has an odd number of elements of order 2. (2) If G is abelian, we compute the sum of the elements of the group (where group multiplication is written as addition).
  1. MathDoctorBob
  2. Mathematics
  3. abstract
  4. algebra
  5. group
  6. theory
Рекомендации по теме
Order 2 Elements 0:07:39

Order 2 Elements in Finite Group

Proof: Finite Order 0:07:58

Proof: Finite Order Elements Have n Distinct Powers | Abstract Algebra

Number of elements 0:20:56

Number of elements of order 2 in a finite group

Understanding the Finite 0:18:36

Understanding the Finite Element Method

(Abstract Algebra 1) 0:09:01

(Abstract Algebra 1) Definition of a Cyclic Group

The order of 0:09:44

The order of every element of a finite group is finite

let g1g2 be 0:05:09

let g1g2 be two elements of a finite group G, then the order of g1g2 is the same as that of g2g1

Group Multiplication Tables 0:07:32

Group Multiplication Tables | Cayley Tables (Abstract Algebra)

300 Tough Questions 1:51:59

300 Tough Questions Of DMS | Lecture-3 | GATE CSE | GATE DA

Finite Element Method 0:00:58

Finite Element Method — Gilbert Strang

Finite Simple Group 0:03:01

Finite Simple Group (of Order Two)

finite order of 0:03:49

finite order of product of two elements Abstract algebra IIT Jam 2015 group theory

RNT1.2.2. Order of 0:05:47

RNT1.2.2. Order of a Finite Field

(Abstract Algebra 1) 0:07:56

(Abstract Algebra 1) Finite Groups

order of every 0:11:31

order of every element of finite group is finite

Order of an 0:04:07

Order of an Element Divides the order of a finite cyclic group Proof (Abstract Algebra)

5. Order of 0:02:47

5. Order of a group || Finite group || Infinite group || Order of finite group #group #orderofagroup

Finite Groups | 0:37:36

Finite Groups | Modern Algebra 1

Number of generators 0:00:58

Number of generators of finite cyclic group|Maths Box|

All you need 0:27:00

All you need to know from finite element theory | Part 2 | variational and weak formulation of PDEs

Abstract Algebra - 0:20:04

Abstract Algebra - 3.1 Finite Groups and Subgroups: Terminology and Notation

TIFR 2017 || 0:06:45

TIFR 2017 || Q.12. There exist a finite abelian group containing exactly 60 elements of order 2 ??

FINITE GROUP & 0:03:35

FINITE GROUP & ORDER OF AN ELEMENT || OU EDUCATION

ORDER OF a 0:06:16

ORDER OF a AND b ARE FINITE BUT ORDER OF ab IS INFINITE

Комментарии
Автор

@candamohcine You're welcome! As you can probably tell, I like group theory and matrices. - Bob

MathDoctorBob
Автор

I am reminded of how 18.100 made my head hurt in the late 1970's... but not as much as 18.701. These videos are great. Keep up the good work!

stephenj.bridges
Автор

we already have exercise from school, now youtube has exercise for us too

lemyul
Автор

If it's not numbered, it was probably filmed long before the numbered vids. Probably requested by someone.

MathDoctorBob
Автор

hello and thanks so much for your videos, i have a question : why do we know that there only those elemets in the group ? why for example we don't have elemets of order 3, in other words why after eliminating e and invese pairs we are left exactly with elements of order 2

amine
Автор

I think these lecture may not be in this position..as this uses the concepts which may be covered in subsequent lecture..

SPDE