filmov
tv
Triangle angle example 1 | Angles and intersecting lines | Geometry | Khan Academy
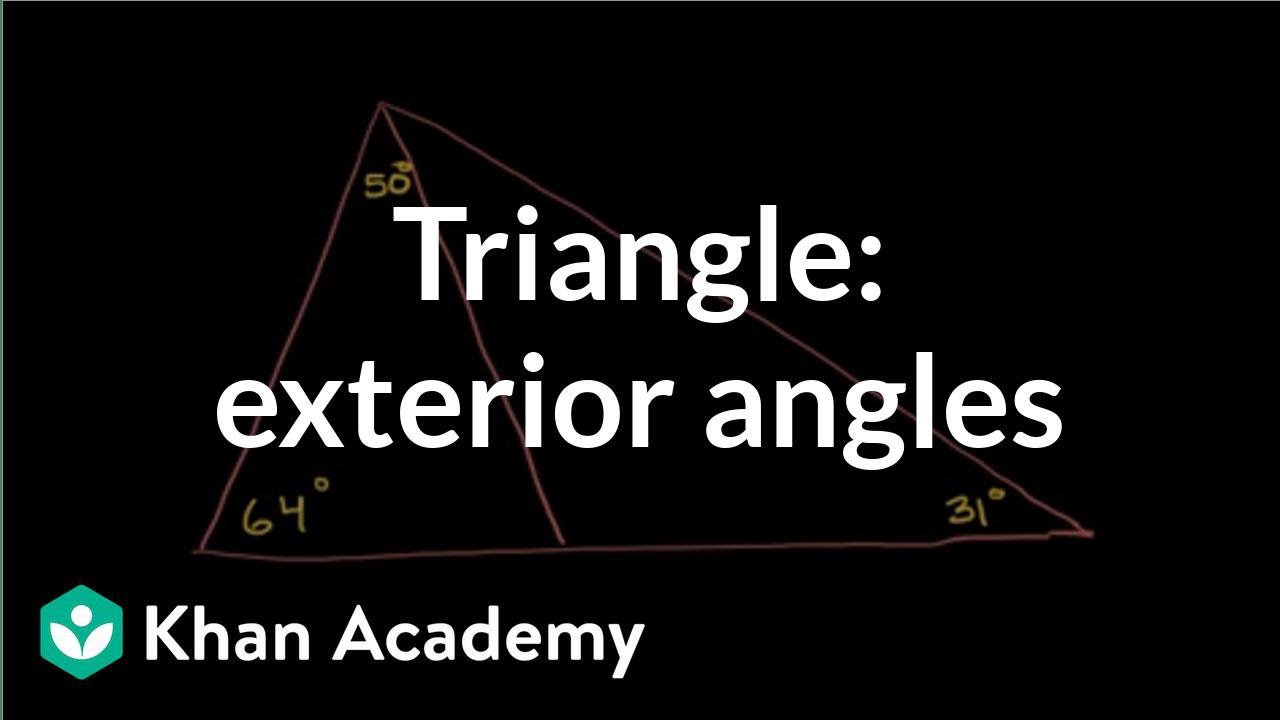
Показать описание
Figuring out angles in a triangle. A little about exterior angles being the sum of the remote interior angles
Missed the previous lesson?
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
Комментарии
 0:06:03
0:06:03
 0:05:14
0:05:14
 0:07:00
0:07:00
 0:04:55
0:04:55
 0:12:41
0:12:41
 0:05:25
0:05:25
 0:14:33
0:14:33
 0:04:28
0:04:28
 0:02:11
0:02:11
 0:01:24
0:01:24
 0:06:40
0:06:40
 0:12:52
0:12:52
 0:01:26
0:01:26
 0:03:54
0:03:54
 0:01:56
0:01:56
 0:02:02
0:02:02
 0:29:56
0:29:56
 0:05:42
0:05:42
 0:00:22
0:00:22
 0:12:37
0:12:37
 0:05:14
0:05:14
 0:01:45
0:01:45
 0:02:00
0:02:00
 0:04:28
0:04:28