filmov
tv
Derivative of y = 3x^3 e^x sinx lnx

Показать описание
In this video, I showed how to apply the product rule to a product of multiple functions
Calculus: Derivative of y = 6^{3x - 4}
find the derivative of y = (4x-1)^3
Find the derivative dy/dx using chain rule for y = x^3 (2x -5)^4
find the derivative of y = (3x-4)(x^3+5) using the product rule
Taking the derivative of two binomials using product and chain rule
find the derivative of y = (3x + 1)^2
Find the derivative dy/dx using chain rule for y = 3/(sqrt(2x +1)).
Find stationary points and sketch the curve of y = x^3 - 3x^2. Calculus
IB Math 2023 AA HL Nov P3 Q1
How to differentiate y = sin(3x) using the Chain Rule
OCR MEI Core 3 4.03 Using the Chain Rule to Differentiate y = (3x - 5)^6
First Principle Differentiation of y = x^3 #excellenceacademy #jonahemmanuel #firstprinciple
Derivative by First principle - Example 3
Chain Rule Steps to Differentiate y = (x^2 + 5)^3
Find equation of tangent line to curve y = x^3 -3x +1 at [2, 3]. Definitions of derivative.
Implicit Differentiation ❖ x^3 - 3x^2y+2xy^2 = 12 ❖ Calculus 1
Find d^3y/dx^3 the third derivative of y = (3x+5)^3
How to Differentiate y = 3x sin2x using the Product Rule
Derivative of 2^3x
Chain rule with radicals, how to take the derivative
Find equation of tangent and normal line to curve y= 3x^2 - x^3 at (1,2). Differentiation
y = 3x^(2/3) find the derivative
find the derivative of 3x^2(x^3 + 1)^7
Differentiate a product y = (x^3)(cos 3x)(ln x)
Комментарии
 0:02:00
0:02:00
 0:00:34
0:00:34
 0:03:38
0:03:38
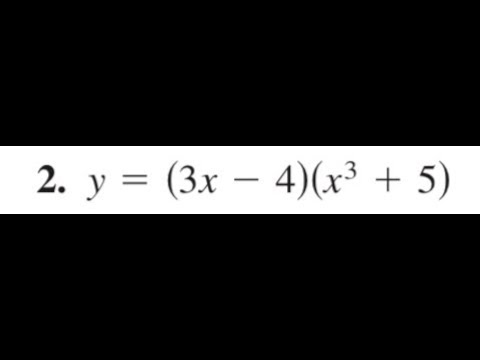 0:00:57
0:00:57
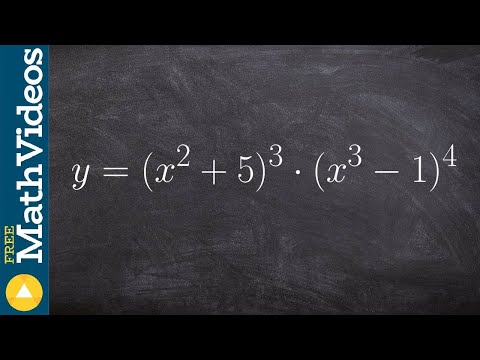 0:04:44
0:04:44
 0:00:47
0:00:47
 0:04:08
0:04:08
 0:05:25
0:05:25
 0:21:49
0:21:49
 0:01:32
0:01:32
 0:03:27
0:03:27
 0:11:42
0:11:42
 0:06:40
0:06:40
 0:02:06
0:02:06
 0:04:12
0:04:12
 0:07:57
0:07:57
 0:02:24
0:02:24
 0:01:48
0:01:48
 0:01:36
0:01:36
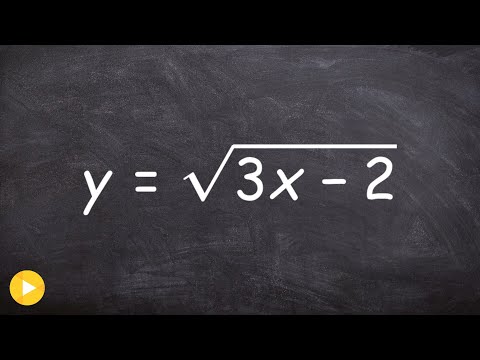 0:01:36
0:01:36
 0:02:41
0:02:41
 0:00:30
0:00:30
 0:00:58
0:00:58
 0:22:06
0:22:06