filmov
tv
Solving Higher Order Polynomials Pt 1 Rational Zeros Descartes Rule

Показать описание
In a 2 part video I show you how to solve equations with a degree larger than 2 without the aid of a graphing calculator or computer.
Solving Higher Order Polynomials Pt 1 Rational Zeros Descartes Rule
Solving Higher Order Polynomial Equations
Solving Higher Order Polynomials Pt 2 Rational Zeros Descartes Rule
Solve higher Order Polynomial Equation by Calculator #shorts
Master how to factor a higher order polynomial by grouping
Solving Higher Order Polynomial Equations
Master Factoring higher order polynomials
Factoring Higher Order Polynomials - Examples - Pre-Calculus
He can factor a cubic trinomial
polynomials super trick to find roots of cubic equation | factorisation trick
Factoring by Grouping #mathteachergon #algebra #factoring #factoringpolynomials
Factoring 3x³ + x² - 15x - 5 #Shorts #algebra #math #maths #mathematics #education #learn #learning...
Solving a Polynomial Equation | jensenmath.ca #maths #math #advancedfunctions
Solve higher Order Polynomial Equation by Calculator #shorts
FASTEST way to factor a trinomial! #shorts
Factoring Higher Order Polynomials
Solving polynomial equations be like
How To Factor a Polynomial to the 5th Degree #shorts
Factor High Order Polynomial in 60 Seconds! #math #maths #mathematics #shorts
Can you solve this cubic equation by factoring?
When mathematicians get bored (ep1)
How to factor and solve 4th degree polynomials
PEMDAS Math Problem | Algebra Fundamentals | JusticeTheTutor #math #shorts #maths #mathstricks
01.05.2011 - Algebra 2 & Trig - Solving Higher Degree Polynomial Equations
Комментарии
 0:14:00
0:14:00
 0:04:40
0:04:40
 0:10:28
0:10:28
 0:00:51
0:00:51
 0:05:41
0:05:41
 0:18:48
0:18:48
 0:13:36
0:13:36
 0:07:56
0:07:56
 0:00:14
0:00:14
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:00:47
0:00:47
 0:00:59
0:00:59
 0:00:48
0:00:48
 0:00:55
0:00:55
 0:10:31
0:10:31
 0:00:17
0:00:17
 0:00:39
0:00:39
 0:01:00
0:01:00
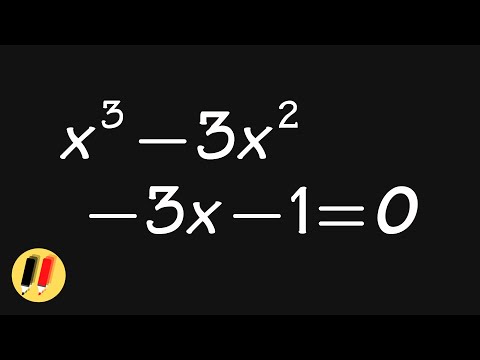 0:00:59
0:00:59
 0:00:37
0:00:37
 0:01:00
0:01:00
 0:00:29
0:00:29
 0:11:52
0:11:52