filmov
tv
Crack the Challenge: Mastering An Incredible Algebra Equation
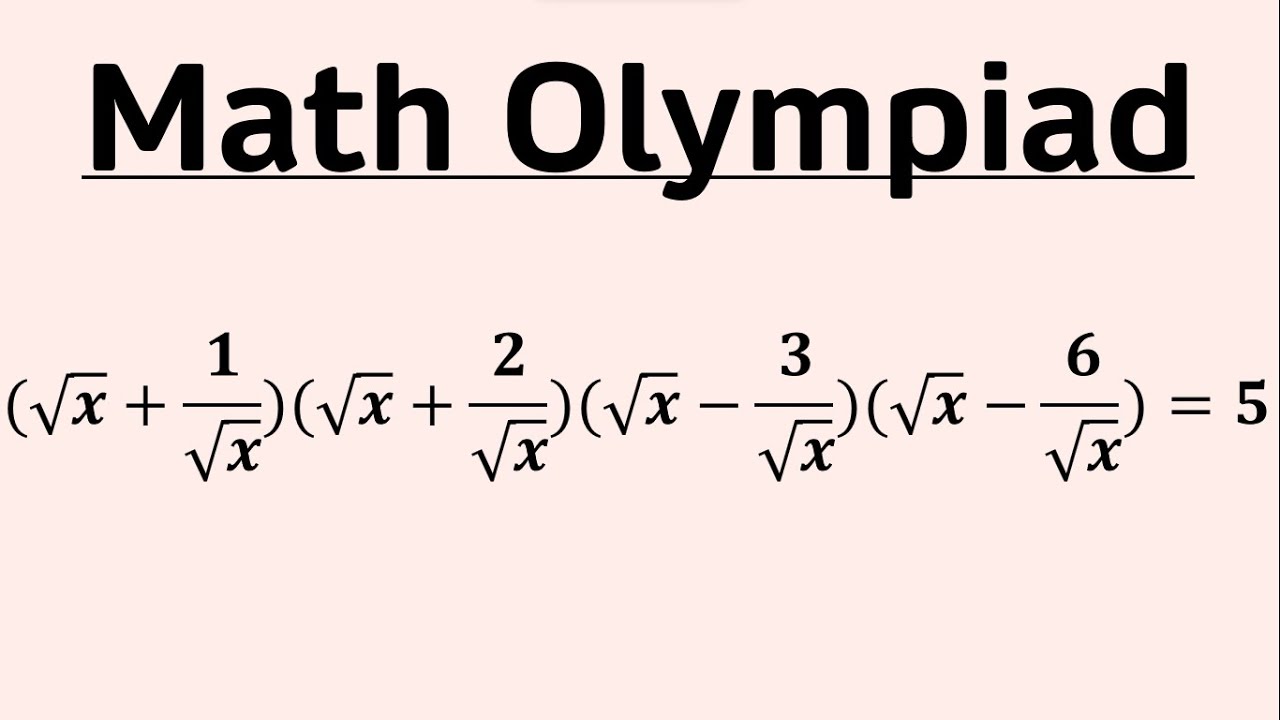
Показать описание
Crack the Challenge: Mastering An Incredible Algebra Equation
Embark on a mathematical journey as we delve into the world of algebraic challenges! In this video, we're tackling an incredible equation that will test your problem-solving skills. Join us to unlock the secrets, master the steps, and crack the challenge together. Get ready to elevate your algebraic prowess!
Topics Covered:
1. Understanding the basics of challenging radical equation from algebra.
2. Analyzing the quartic equation using algebraic tricks.
3. Step-by-step approach to solving the algebraic quartic equation.
4. Tips and tricks for handling tricky radicals like a pro.
5. Algebraic identities and manipulations while solving equations.
Timestamps:
0:00 Introduction
0:40 Domain
2:25 Solving Quartic equation
2:45 Algebraic manipulations
5:44 Algebraic identities
8:49 Solving quadratic equations
9:58 Quadratic formula
11:15 Solutions
#AlgebraChallenge #Mathematics #ProblemSolving #EquationMastery #CrackTheChallenge #MathEnigma #MathPuzzle #AlgebraSkills #MathJourney #MasteringMath #ProblemSolvingSkills #algebra #algebrachallenge #maths #mathenthusiast #radical #quarticequation
This video is perfect for students, math enthusiasts, or anyone seeking to sharpen their problem-solving skills and gain confidence in dealing with radical equations. 🎓📈
🔔 Challenge yourself and see if you can solve the equation before we do! Hit the like button if you're up for the challenge and remember to subscribe for more exhilarating math content! 🛎️🔔
Don't forget to like, comment, and subscribe to join our math-loving community. Let's get started on this exciting journey together! 🤝🌟
Thanks for Watching!
@infyGyan
Embark on a mathematical journey as we delve into the world of algebraic challenges! In this video, we're tackling an incredible equation that will test your problem-solving skills. Join us to unlock the secrets, master the steps, and crack the challenge together. Get ready to elevate your algebraic prowess!
Topics Covered:
1. Understanding the basics of challenging radical equation from algebra.
2. Analyzing the quartic equation using algebraic tricks.
3. Step-by-step approach to solving the algebraic quartic equation.
4. Tips and tricks for handling tricky radicals like a pro.
5. Algebraic identities and manipulations while solving equations.
Timestamps:
0:00 Introduction
0:40 Domain
2:25 Solving Quartic equation
2:45 Algebraic manipulations
5:44 Algebraic identities
8:49 Solving quadratic equations
9:58 Quadratic formula
11:15 Solutions
#AlgebraChallenge #Mathematics #ProblemSolving #EquationMastery #CrackTheChallenge #MathEnigma #MathPuzzle #AlgebraSkills #MathJourney #MasteringMath #ProblemSolvingSkills #algebra #algebrachallenge #maths #mathenthusiast #radical #quarticequation
This video is perfect for students, math enthusiasts, or anyone seeking to sharpen their problem-solving skills and gain confidence in dealing with radical equations. 🎓📈
🔔 Challenge yourself and see if you can solve the equation before we do! Hit the like button if you're up for the challenge and remember to subscribe for more exhilarating math content! 🛎️🔔
Don't forget to like, comment, and subscribe to join our math-loving community. Let's get started on this exciting journey together! 🤝🌟
Thanks for Watching!
@infyGyan
Комментарии
 0:11:39
0:11:39
 0:00:26
0:00:26
 0:02:50
0:02:50
 0:02:56
0:02:56
 0:00:54
0:00:54
 0:03:31
0:03:31
 0:00:08
0:00:08
 0:11:56
0:11:56
 0:34:33
0:34:33
 0:05:55
0:05:55
 0:00:13
0:00:13
 0:00:50
0:00:50
 0:00:59
0:00:59
 0:00:11
0:00:11
 0:00:21
0:00:21
 0:00:51
0:00:51
 0:00:50
0:00:50
 0:00:14
0:00:14
 0:00:35
0:00:35
 0:00:08
0:00:08
 0:00:30
0:00:30
 0:00:12
0:00:12
 0:00:49
0:00:49
 1:49:21
1:49:21