filmov
tv
1.4.7 Suppose a b c and d are integers. Prove that a) 2a - 1 is odd b) if a is even then a+1 is odd

Показать описание
Problem 1.4.7 From Smith/Eggen's A Transition to Advanced Mathematics 7th edition from chapter 1, logic and proofs - basic proof methods I.
Enjoy, and I am available for tutoring and private classes! :)
Suppose a, b, c, and d are integers. Prove that
(a) 2a - 1 is odd.
(b) if a is even, then a + 1 is odd.
(c) if a is odd, then a + 2 is odd.
(d) a(a+1) is even.
(e) 1 divides a.
(f) a divides a.
(g) if a and b are positive and a divides b, then a ≤ b
(h) if a divides b, then a divides bc.
(i) if a and b are positive and ab = 1 then a = b = 1
(j) if a and b are positive, a divides b and b divides a, then a = b
(k) if a divides b and c divides d, then ac divides bd.
(l) if ab divides c, then a divides c.
(m) if ac divides bc, then a divides b.
Enjoy, and I am available for tutoring and private classes! :)
Suppose a, b, c, and d are integers. Prove that
(a) 2a - 1 is odd.
(b) if a is even, then a + 1 is odd.
(c) if a is odd, then a + 2 is odd.
(d) a(a+1) is even.
(e) 1 divides a.
(f) a divides a.
(g) if a and b are positive and a divides b, then a ≤ b
(h) if a divides b, then a divides bc.
(i) if a and b are positive and ab = 1 then a = b = 1
(j) if a and b are positive, a divides b and b divides a, then a = b
(k) if a divides b and c divides d, then ac divides bd.
(l) if ab divides c, then a divides c.
(m) if ac divides bc, then a divides b.
 0:04:31
0:04:31
 0:05:45
0:05:45
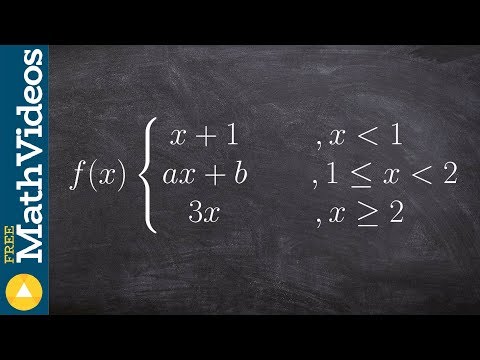 0:03:44
0:03:44
 0:10:10
0:10:10
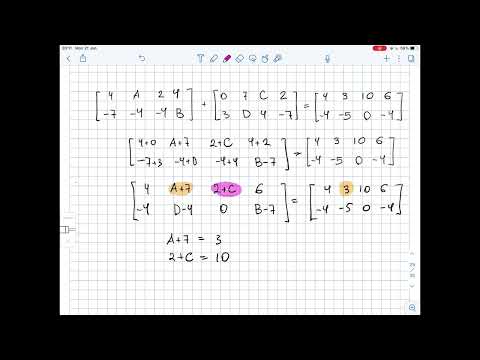 0:02:24
0:02:24
 0:00:33
0:00:33
 0:14:06
0:14:06
 0:04:27
0:04:27
 0:02:32
0:02:32
 0:08:05
0:08:05
 0:05:00
0:05:00
 0:07:24
0:07:24
 0:05:48
0:05:48
 0:06:16
0:06:16
 0:02:50
0:02:50
 0:03:45
0:03:45
 0:01:03
0:01:03
 0:01:54
0:01:54
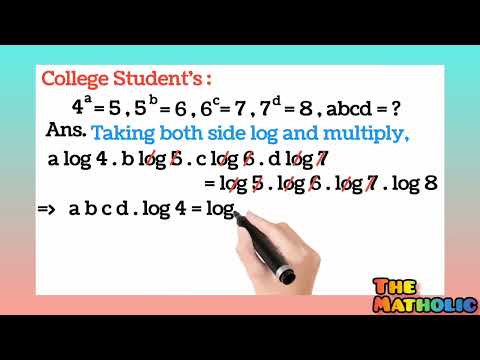 0:02:33
0:02:33
 0:02:39
0:02:39
 0:12:14
0:12:14
 0:10:38
0:10:38
 0:03:19
0:03:19
 0:03:37
0:03:37