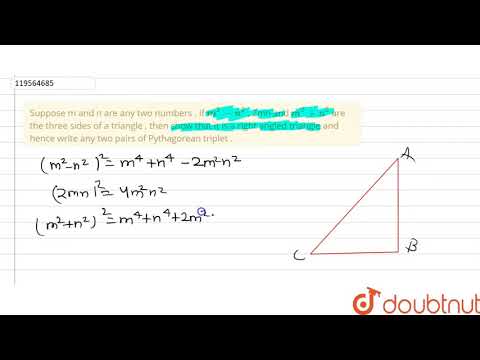
Suppose that ‘n’ number and I, F are integral part, frac S.T. i) I is odd integer ii) (I+F)(1-F)=1

Welcome to this exciting video about number theory and algebra! In this video, we are going to explore a fascinating problem in number theory that involves powers of complex numbers, integral and fractional parts of numbers, and odd integers.

Let us start with the problem statement. Suppose that ‘n’ is a natural number and I, F are integral part and fractional part of (7 + 4sqrt 3)^ n. We want to find the following two conditions:

i) I is odd integer
ii) (I + F)(1 - F) = 1

The first condition requires us to find the integral part of a complex number raised to the power of ‘n.’ In this case, the complex number is (7 + 4sqrt 3), and we want to raise it to the power of ‘n.’ To find the integral part of the result, we need to discard the fractional part of the number. The fractional part is denoted by F.

The second condition involves both the integral and fractional parts of the number. We need to find a relationship between I and F that satisfies the equation (I + F)(1 - F) = 1. This relationship will help us to understand the properties of the number (7 + 4sqrt 3) raised to the power of ‘n.’

Before we dive into the solution, let us take a moment to understand some of the basic concepts related to complex numbers, integral and fractional parts, and odd integers.

A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit, which is defined as the square root of -1. In the problem statement, the complex number is (7 + 4sqrt 3).

The integral part of a number is the largest integer that is less than or equal to the number. For example, the integral part of 3.7 is 3, and the integral part of -2.3 is -3. In the problem statement, we want to find the integral part of (7 + 4sqrt 3)^ n.

The fractional part of a number is the difference between the number and its integral part. For example, the fractional part of 3.7 is 0.7, and the fractional part of -2.3 is 0.7. In the problem statement, we want to find the fractional part of (7 + 4sqrt 3)^ n.

An odd integer is an integer that is not divisible by 2. For example, 3, 5, 7, and 9 are odd integers, while 2, 4, 6, and 8 are not. In the problem statement, we want to find an odd integer for the integral part of (7 + 4sqrt 3)^ n.

Now, let us move on to the solution of the problem. To find the integral and fractional parts of (7 + 4sqrt 3)^ n, we can use the binomial theorem. The binomial theorem is a formula that can be used to expand expressions of the form (a + b)^ n, where ‘a’ and ‘b’ are any real numbers, and ‘n’ is a positive integer. The binomial theorem states that:

(a + b)^ n = C(n, 0) a^n b^0 + C(n, 1) a^(n-1) b^1 + C(n, 2) a^(n-2) b^2 + ... + C(n, n-1) a^1 b^(n-1) + C(n, n) a^0 b^n
#mathproblems #numbertheory #algebra #complexnumbers #binomialtheorem #integrals #fractionals #oddintegers #mathvideos #matheducation #mathhelp #mathematical #mathnerd #mathgeek #mathisfun #mathstagram #learnmath #solveproblems #problemssolving #mathskills #mathematician #mathematicalthinking #mathconcepts #mathsolutions #mathproblemsolving #mathformulas #mathformulae #mathresources #mathknowledge #mathlearning #mathstudy #mathstudents #mathematics
where C(n, k) is the binomial coefficient, which
contact : [phone](whatsapp)
whatsapp :[phone]

[ManasaPinniboina]

Nice explanation sir ...chala clarity gaa cheparu .. thankyou sir😃😊❤️

[zareenabegum]

Sir na life lo entha clarity ga explain chesindi meru okka re sir thank you so much sir😊

[ImranKhan-rgqx]

At 7:40 minutes F is fraction part of (7+4root 3 )^n know sir .Then why F range is zero to one .