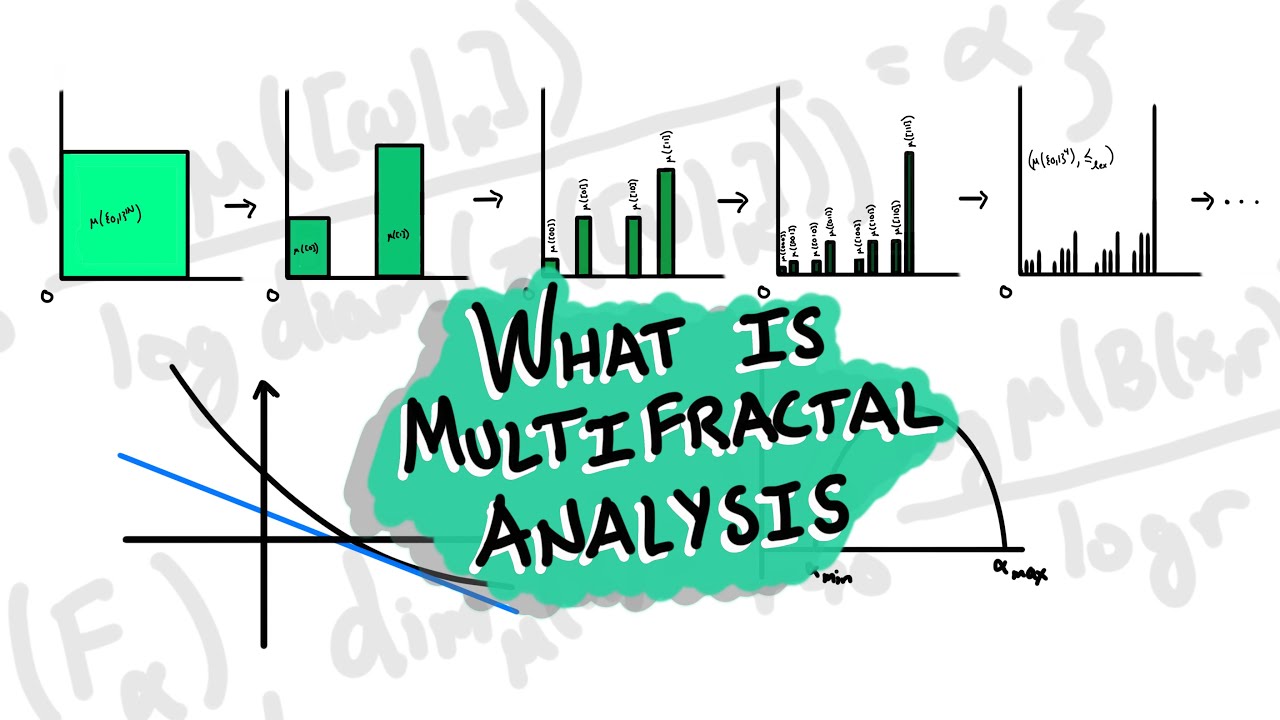
What is Multifractal Analysis? Modern Fractal Geometry and my research

Hausdorff dimension is not a fine enough analysis for many objects of interest in modern fractal geometry. Luckily Hausdorff dimension can be adapted to the study of multifractals or a multifractal decomposition via multifractal analysis. This area of modern fractal geometry is core to my math phd research area for my dissertation, and so I wanted to spend a bit of time trying to communicate a bit about it here. In the process we'll connect fractal constructions and measure theory to generate a "irregular" fractal where such a multifractal analysis is required and then give an overview of what such an analysis would involve.

00:00 Intro
00:14 What is studied in fractal geometry?
03:10 A fractal with "irregularity"
07:11 Nathan's mid video math comm crisis
07:58 A multifractal analysis with respect to local dimension

______

______

WHAT GEAR I USED FOR THIS VIDEO:

DISCLAIMER: Links included in this description may be affiliate links. If you purchase a product or service with the links that I include here, I may receive a small commission. There is no additional charge to you! Thank you for supporting my channel and for helping me create these free videos!

Subscriber Count as of last CHALK video:

=====

[iamtraditi]

Great video! Thanks for sharing this :)

[lenoel]

Interesting stuff you get to spend your time on!

[ameliaC-xgrg]

Good video! Have you considered making them longer?

[Problemathic]

This is very interesting! Have you done this type of analysis for other dimensions? Immediately come to mind the generalised Hausdorff dimension (defined with gauge functions), box, Assouad, etc

[soupy]

Another field I didn't know about but sounds cool!

[JakubWaniek]

Cool video! I've been thinking of making a video explaining my research too. Do you have any advice about this? In particular, who is your target audience (what background knowledge are you happy to assume?) and what do you do about stuff that seems too technical to be covered well? I find myself in a particularly abstract, categorical corner of representation theory and, to be honest, I don't even know how I'm supposed to motivate what I'm doing to someone who doesn't already at least buy into representation theory as a worthwhile thing to study

[abrahammasaryk]

Doesn't Mendlebrodt define a fractal explicitly as a set where Dh>Dt?

[KilgoreTroutAsf]

5:30 is it possible to define an entropy for the mass localization? as in the average number of bits necessary to find the open set