filmov
tv
A non-standard logarithmic equation
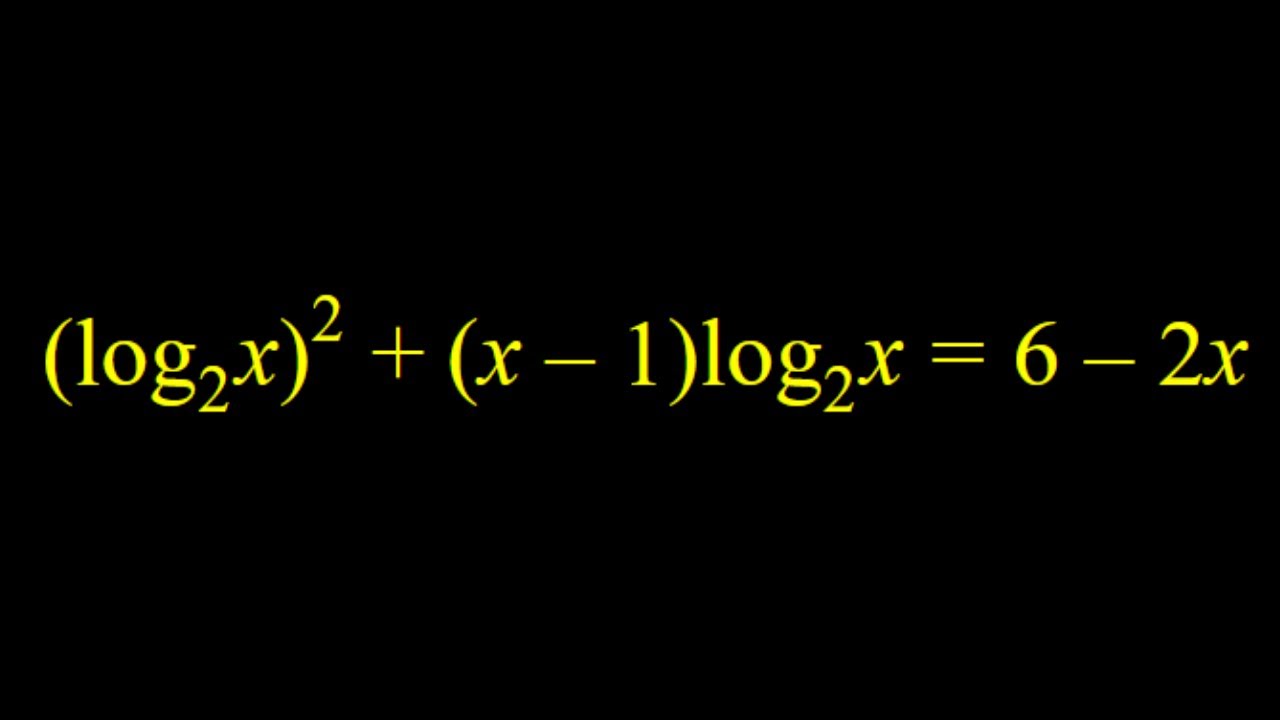
Показать описание
This video is about an extraordinary logarithmic equation whose solution method is unique.
challenging math problems, logarithmic equations, substitution, non-standard problem.
challenging math problems, logarithmic equations, substitution, non-standard problem.
A non-standard logarithmic equation
A Non-Standard Equation with Natural Logarithm
A Non-standard Logarithmic Equation with Different Bases
A Non standard Logarithmic Equation with Different Bases
Solving non-standard EXPONENTIAL equation x^ln(x)=3
Solving Logarithmic Equations
A Non-Standard Equation With One Solution
A Non-standard Exponential Equation
Math 1175-05 - 29 August 2024 - Section 7.3
A Non-Standard Equation | ln(x)=1/2-x
Let's Solve A Nonstandard Equation | Properties of Logs
How to Write a Logarithmic Equation in Exponential Form an Example with a Fraction
Writing Logarithmic Equations In Exponential Form
A Non-standard Equation with e and Logs
SOLVE THIS non-standard EXPONENTIAL equation x^ln(x)=3 #maths #equation #matholympiad
A Non-Standard Exponential System
A Non-Standard Equation with One Solution (k is positive)
Solving A Non-Standard Equation
A Non-Standard Golden Exponential Equation
Solving a logarithmic equation when the bases are different. An algebraic challenge.
LOGARITHMIC/RADICAL EQUATION!!! (Challenging math problem #15)
Logarithmic Equation With Extraneous Solution
Solving a Non-Standard Equation For Reals
SOLVING LOGARITHMIC EQUATIONS || FINDING THE VALUE OF X
Комментарии
 0:08:11
0:08:11
 0:09:56
0:09:56
 0:12:54
0:12:54
 0:12:54
0:12:54
 0:02:29
0:02:29
 0:25:27
0:25:27
 0:09:22
0:09:22
 0:04:35
0:04:35
 1:06:20
1:06:20
 0:05:39
0:05:39
 0:08:15
0:08:15
 0:00:22
0:00:22
 0:03:07
0:03:07
 0:08:42
0:08:42
 0:00:14
0:00:14
 0:09:59
0:09:59
 0:08:42
0:08:42
 0:09:05
0:09:05
 0:09:12
0:09:12
 0:05:06
0:05:06
 0:01:04
0:01:04
 0:05:11
0:05:11
 0:04:34
0:04:34
 0:14:27
0:14:27