filmov
tv
x^2-4x=0 ecuaciones cuadraticas , segundo grado incompletas , conjunto solucion

Показать описание
ecuaciones cuadraticas
ecuaciones de segundo grado
ecuaciones con exponente 2
como hallar x en una ecuacion cuadratica incompletas
ecuaciones de segundo grado
ecuaciones con exponente 2
como hallar x en una ecuacion cuadratica incompletas
x^2-4x=0 ecuaciones cuadraticas , segundo grado incompletas , conjunto solucion
x^2+4x=0 ecuaciones cuadraticas , segundo grado incompletas , conjunto solucion
20x^2+4x=0 , ecuacion cuadratica de 2 terminos, hallar x , segundo grado , exponente 2
2x^2+4x=0 ecuaciones cuadraticas , segundo grado incompletas , conjunto solucion
20x^2-4x=0 , ecuacion cuadratica de 2 terminos, hallar x , segundo grado , exponente 2
8x^2+4x=0 , ecuacion cuadratica de 2 terminos, hallar x , segundo grado , exponente 2
Ecuación de segundo grado incompleta c=0 | x^2-4x=0
2x^2-4x=0 ecuaciones cuadraticas , segundo grado incompletas , conjunto solucion
Álgebra - Semana 04 - Pre San Marcos Ciclo 2022-II
x^2 + 4x = 0
16x^2-4x=0 , ecuacion cuadratica de 2 terminos, hallar x , segundo grado , exponente 2
x^2-4x+4=0 ecuacion cuadratica , grado 2 , segundo grado , x2-4x+4=0
x^2-4x+4=0 Formula general a una ecuacion cuadratica ( 2 grado ) , solucion procedimiento
x^2+4x+4=0 Formula general a una ecuacion cuadratica ( 2 grado ) , solucion procedimiento
x^2-4x-2=0 . Ecuaciones cuadraticas x2-4x-2=0 aplicando formula general , x al cuadrado
x^2+4x-4=0 . Ecuaciones cuadraticas x2+4x-4=0 aplicando formula general , x al cuadrado
x^2+4x+3=0 ecuacion cuadratica , grado 2 , segundo grado , x2+4x+3=0
x^2+4x-2=0 . Ecuaciones cuadraticas x2+4x-2=0 aplicando formula general , x al cuadrado
x^2-4x-10=0 . Ecuaciones cuadraticas x2-4x-10=0 aplicando formula general , x al cuadrado
Ecuaciones cuadráticas incompletas. Por factorización por factor común
x^2+4x=0 Solve the Equation
4x^2-16=0 , ecuaciones cuadraticas , hallar x con exponente 2
x^2-4x-32=0 Formula general a una ecuacion cuadratica ( 2 grado ) , solucion procedimiento
Solución de ecuación cuadrática de 2x²-3x=0
Комментарии
 0:01:01
0:01:01
 0:00:58
0:00:58
 0:01:45
0:01:45
 0:01:18
0:01:18
 0:01:39
0:01:39
 0:01:48
0:01:48
 0:02:33
0:02:33
 0:01:06
0:01:06
 1:49:03
1:49:03
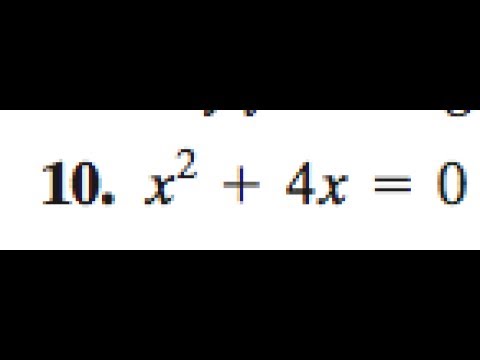 0:00:32
0:00:32
 0:01:43
0:01:43
 0:01:46
0:01:46
 0:02:19
0:02:19
 0:02:05
0:02:05
 0:03:05
0:03:05
 0:02:53
0:02:53
 0:01:43
0:01:43
 0:03:01
0:03:01
 0:02:59
0:02:59
 0:10:36
0:10:36
 0:01:08
0:01:08
 0:01:13
0:01:13
 0:02:19
0:02:19
 0:01:07
0:01:07