filmov
tv
IB Math AA 2021 Nov TZ0 Paper 1 SL Question 8 - Log and Sequence

Показать описание
Also check out my membership for a full course and sorted past paper
IB Math AA SL TZ0 Nov 2021 Paper 1: Read the question, dammit
IB Math AA HL Nov 21 TZ0 Paper 1: Integrating Factors Are Smelly
IB Math AA 2021 Nov TZ0 Paper 1 SL Question 8 - Log and Sequence
IB Math AA 2021 Nov TZ0 Paper 1 SL Question 9 - Differentiation and Integration
IB Math AA 2021 Nov TZ0 Paper 1 HL Question 1 SL Question 2 - Integration
IB Math AA 2021 Nov TZ0 Paper 1 SL Question 7 HL Question 10 - Kinematics
IB Math AA 2021 Nov TZ0 Paper 2 HL Question 8 - Differentiation
IB Math AA 2021 Nov TZ0 Paper 1 HL Question 5 SL Question 5 - Differentiation
IB Math AA HL 2021 Nov TZ0 Paper 3 Question 1
IB Math AA SL Nov 2021 TZ0 Paper 2: Avocado's Number
IB Math AA 2021 Nov TZ0 Paper 2 HL Question 10 - Function and Integration
IB Math AA 2021 Nov TZ0 SL Question 4 HL Question 3 - Binomial Distribution
IB Math AA HL 2021 Nov TZ0 Paper 3 Question 2
IB Math AA 2021 Nov TZ0 Paper 1 HL Question 12 - Complex Number
IB Math AA SL 2021 Nov TZ0 Paper 1 Preview
IB Math AA 2021 Nov TZ0 Paper 2 HL Question 7 - Random Variable
IB Math November 2021 AA HL Past Paper 1 Q3.
IB MATH NOV 2021| Analysis & Approaches AA HL PAPER 1 TZ0 | PART 2- QUESTIONS 7-12 (with timesta...
IB DP Math AA HL Paper 3 N21 ( November 2021 ) Full Solutions with Solving Strategy
IB Math AA 2021 Nov TZ0 Paper 2 SL Question 9 - Normal Distribution
IB Math AA 2021 Nov TZ0 Paper 2 SL Question 8 HL Question 9 - Tri Graph
IB Math AA 2021 Nov TZ0 Paper 2 SL Question 2 - function
IB Math AA 2021 Nov TZ0 Paper 1 HL Question 7 - Quadratics
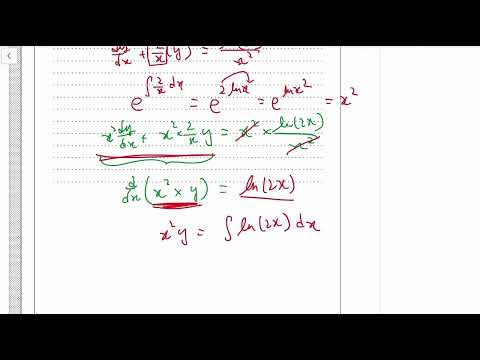
IB Math AA 2021 Nov TZ0 Paper 1 HL Question 8 - Differential Equation
Комментарии
 1:29:48
1:29:48
 1:36:51
1:36:51
 0:11:15
0:11:15
 0:09:29
0:09:29
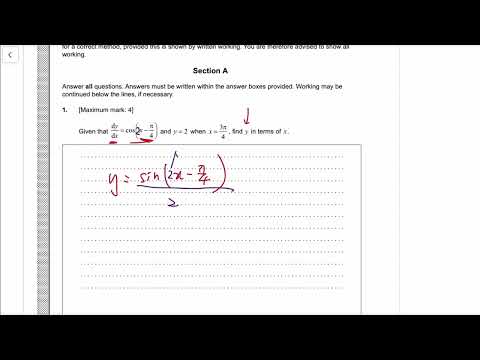 0:02:14
0:02:14
 0:10:20
0:10:20
 0:06:16
0:06:16
 0:07:26
0:07:26
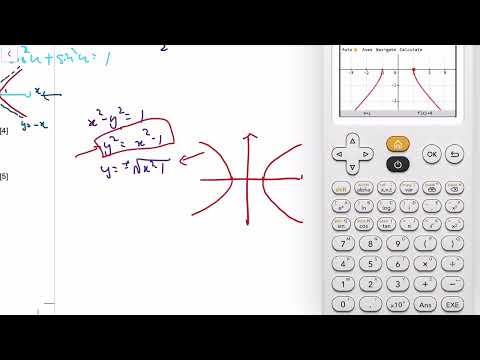 0:17:15
0:17:15
 1:41:42
1:41:42
 0:12:02
0:12:02
 0:05:06
0:05:06
 0:17:11
0:17:11
 0:11:05
0:11:05
 0:01:15
0:01:15
 0:04:38
0:04:38
 0:03:18
0:03:18
 1:03:17
1:03:17
 0:31:54
0:31:54
 0:19:47
0:19:47
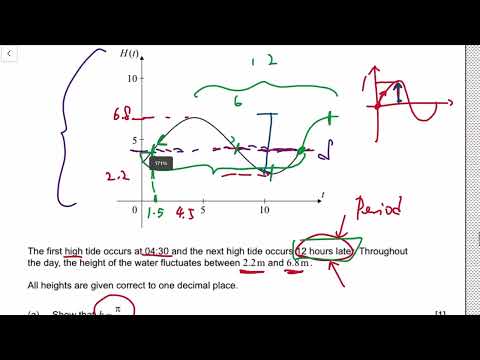 0:12:41
0:12:41
 0:01:05
0:01:05
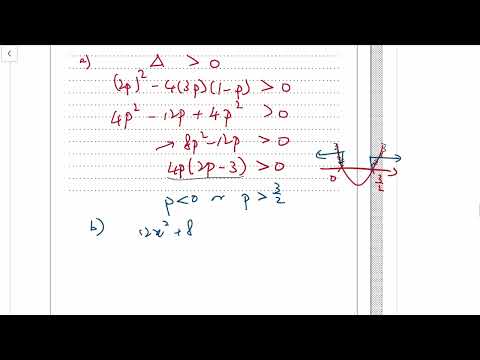 0:03:34
0:03:34
 0:05:11
0:05:11