Order fractions with the same numerator

So we have 1 fifth, 1 quarter and 1 eighth, and we need to write these fractions in order, smallest first. So the important thing to remember about fractions is that the larger the denominator, the smaller the fraction – that’s because your whole has been divided into more pieces, so each piece is smaller. Now, all of these fractions have the same numerator, so here, we’re just looking at the denominator of each fraction. So which of these is the smallest? []1 eighth is the smallest, then 1 fifth, then 1 quarter. Now, it seems strange that fractions with larger denominators are smaller, so let’s look at 1 eighth, 1 fifth and 1 quarter, so that we can see how small or large they are. []You can see clearly here that 1 eighth is the smallest. That’s because, if our rectangle has been divided into 8 pieces and we only have 1 piece, the piece that we have left – the piece shaded in blue here – is small. Then we have 1 fifth in the middle, and 1 quarter is our largest fraction – and you might be able to spot here that 1 quarter is twice the size of 1 eighth – we would need 2 eighths to have the same amount shaded blue as we have in 1 quarter.[]
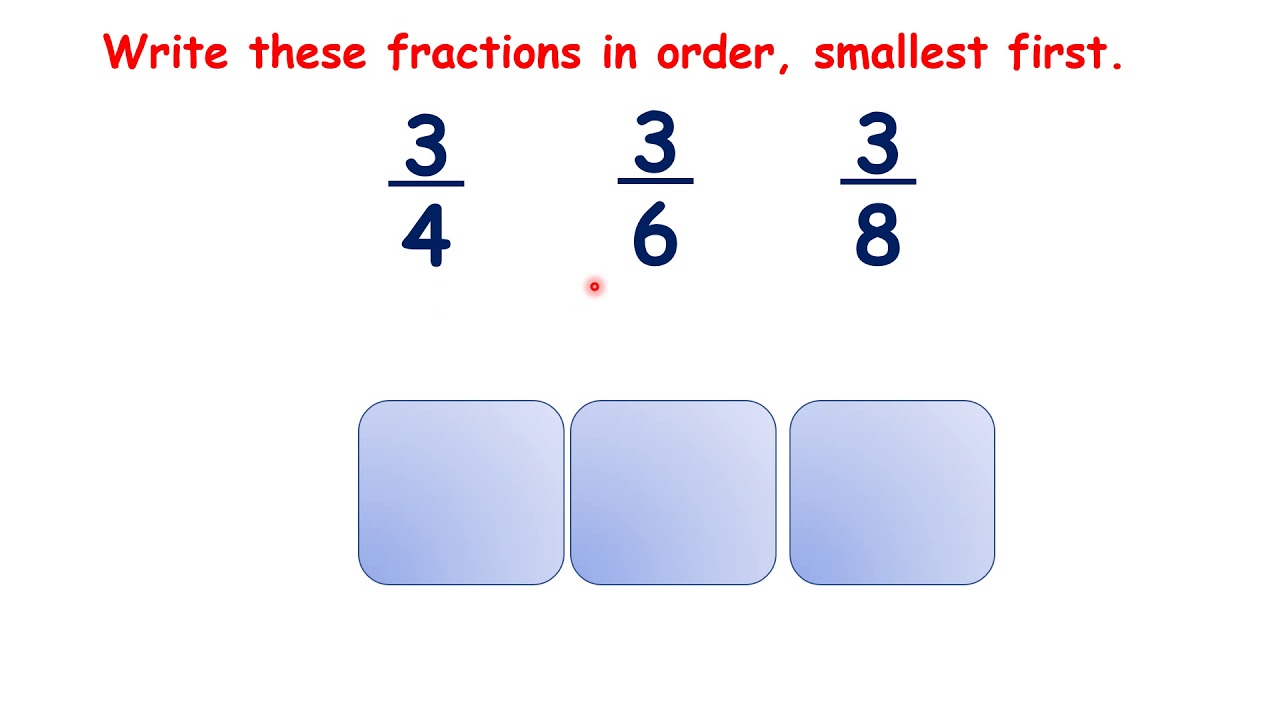
Now let’s try 3 quarters, 3 sixths and 3 eighths. Although we don’t have 1 in the numerator, we do have the same numerator for all of our fractions: they all have 3 as the numerator. So all we need to remember is that the larger the denominator, the smaller the fraction. So which is our smallest fraction? It’s the fraction with the largest denominator, []so 3 eighths. What do we have next? []We have 3 sixths. And that means our largest fraction is []3 quarters. Again, it will help us to see the fractions – and when you’re ordering fractions, it’s useful to picture in your mind what each one looks like. So let’s look at 3 eighths, 3 sixths and 3 quarters. []You can see that even though we have 3 pieces, because 3 is the numerator, for all of our fractions, the pieces are different sizes for each fraction. Because this top rectangle has been divided into more pieces, each piece is smaller, and because this bottom rectangle has not been divided into as many pieces, each piece is larger.