Degree Sequence of a Graph | Graph Theory, Graphical Sequences

What is a degree sequence of a graph? Are graphs with the same degree sequence isomorphic? Do isomorphic graphs have the same degree sequence? We’ll go over all of this in today’s video graph theory lesson!

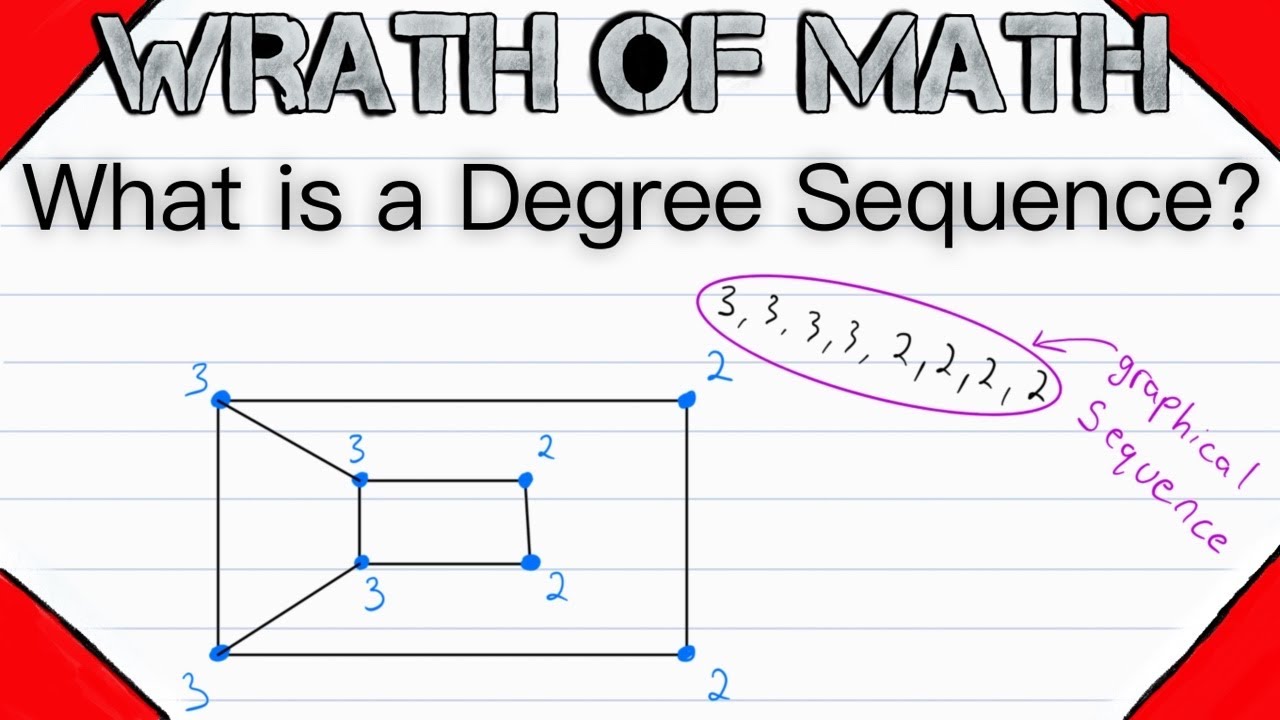
Recall that the degree of a vertex is the number of edges incident to the vertex. If we list the vertex degrees of a graph in a sequence, that sequence is called a degree sequence. By some definitions, a degree sequence has to be non-increasing, meaning each degree in the sequence is greater than or equal to the next degree. The nice thing about that definition is it makes the degree sequence of each graph unique, so there is only one degree sequence for each graph! As I always say, be aware of the definition being used since there are multiple in use for this term.

It is clear that if two graphs are isomorphic, they must have the same degree sequences. We do not prove this in the lesson but we do look at a small example of it. The converse is more interesting and not true. If two graphs have the same degree sequences they are not necessarily isomorphic, and we will see an interesting example of that!

Of course it is clear that every graph has at least one degree sequence, but is every finite sequence of nonnegative integers the degree sequence of some graph? If a sequence is a degree sequence of some graph, we call it graphical. So is every finite sequence of nonnegative integers graphical? What do you think? Watch the full video lesson for more!

Here is an example of a finite sequence of nonnegative integers that is not graphical: 1, 0. Such a graph would need to have two vertices, call them x and y. Suppose x has degree 1, then it must be adjacent to y, which means both x and y have degree 1. Clearly, no graph exists with two vertices, one of degree 1, and the other degree 0. More generally, if a sequence of length n has a 0 in it, and it has n-1 in it, then it cannot be graphical. Because if a graph has n vertices and a vertex has degree n-1, that means it is adjacent to every other vertex in the graph, so every other vertex must have degree at least 1. Thus, there cannot be a degree of 0 in such a graph.

If you're taking a course in Graph Theory, or preparing to, you may be interested in the textbook that introduced me to Graph Theory: “A First Course in Graph Theory“ by Gary Chartrand and Ping Zhang. It’s a wonderful text! You can purchase this book through my Amazon affiliate link below! Using the affiliate link costs you nothing extra, and helps me continue to work on Wrath of Math!

I hope you find this video helpful, and be sure to ask any questions down in the comments!

********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.

********************************************************************

+WRATH OF MATH+

Follow Wrath of Math on...

[WrathofMath]

Support the production of this course by joining Wrath of Math as a Channel Member for exclusive and early videos, original music, and upcoming lecture notes for the graph theory series! Plus your comments will be highlighted for me so it is more likely I'll answer your questions!

[adarshsaurabh]

This explanation is awesome really awesome its like fire

[PunmasterSTP]

Graphical sequences? More like "Great videos; thank you for teaching us!" 🙏

[ronaldcsjohnson]

To be graphic, do the graph also have to be a simple graph?

3, 3 can be a degree sequence of a multigraph.

[christiancarter]

How would I graph degree sequence 5, 4, 4, 3, 2, 2 ?

[k_gold]

This question made so many i know fail semester, this is a lot of information for a basic engineering subject. Hope they remove this in future syllabus

[saanyalakhani]

What will be the degree sequence of a graph with 3 vertices?

[djsnowpdx]

I aspire to teach math with Notability as well as you do!

[amirsohail]

Does every sequence have simple graph? Explain why?

[anarojas]

Could a simple graph be made, say with 6 vertices and a degree sequence of (1, 0, 0, 0, 0, 0, 0)? From what I can gather is that for n-vertices, deg(v)={(deg(v1), deg(v2), ...deg(v_n)} where i=1, 2, ..., n-1 we can form a simple graph, correct? There is also the fact that the sum of the degree sequence which is odd, hence no simple graph.

[bharathsimha]

Plz do videos about theroms on trees and eulerian graphs

[midhilak]

can't the sequence 3, 3 be a degree sequence of a multigraph with 2 self loop??

[kurtmueller]

So does a graph thats unconnected have a continuous degree sequence?

[nahlaabouchakra]

A finite sequence of non-negative integers is graphical if the sum of degrees is twice number of edges which means also that the sum should be even

[mohammad_bilal]

Can you explain this one ?
Degree of a graph δ(G). What is it ?
does degree of a graph means "degree sequence" of a graph ?

[LearningCS-jpcb]

1, 2, 3, ..., n can never be graphical, as seen in proof of irregular graphs. Party theorem states atleast 2 vertices should have same degree.