filmov
tv
Understanding Expected Value vs Average | Explained by Michael

Показать описание
We delve into the difference between an expected value and the average, looking at a case where they are the same and cases where they differ.
This is the 2nd video in a series on understanding topics conceptually in probability and statistics. When we understand the root level, formulas often no longer are worrisome and difficult.
This is the 2nd video in a series on understanding topics conceptually in probability and statistics. When we understand the root level, formulas often no longer are worrisome and difficult.
Understanding Expected Value vs Average | Explained by Michael
Expected Values, Main Ideas!!!
What's the connection between Arithmetic Mean & Expected Value?
Mean (expected value) of a discrete random variable | AP Statistics | Khan Academy
Expected Value Explained Intuitively
How To Calculate Expected Value
Expected Value and Variance of Discrete Random Variables
Understanding Expectation of a Random Variable: Intuition for Expected Value and Linearity
Expected Values for Continuous Variables!!!
Mean & Expected Value - Probability
L05.8 Expectation
Expectation of a Random Variable Equation Explained
The Expected Value and Variance of Discrete Random Variables
Expected Value Example and Intuitive Explanation
How to Calculate the Mean, or Expected Value, of a Continuous Random Variable
But what is the Central Limit Theorem?
Expected Value or Mean of Probability Distribution || Lesson 47 || Probability & Statistics ||
The Standard Deviation (and Variance) Explained in One Minute: From Concept to Definition & Form...
Wavefunction Properties, Normalization, and Expectation Values
L05.10 The Expected Value Rule
What is an Expectation Value? Quantum Jargon Explained
Expected Value, Variance & Standard Deviation
Expected Value - Mastering AMC 10/12
Expected Value
Комментарии
 0:10:23
0:10:23
 0:13:39
0:13:39
 0:03:29
0:03:29
 0:04:32
0:04:32
 0:09:08
0:09:08
 0:07:00
0:07:00
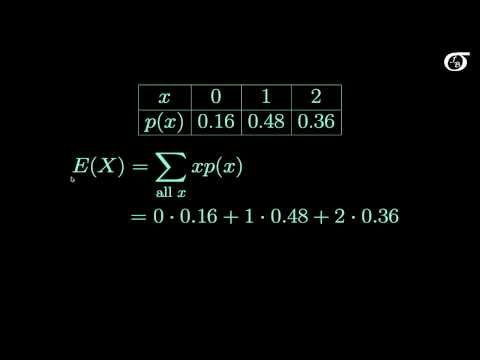 0:07:57
0:07:57
 0:07:02
0:07:02
 0:19:44
0:19:44
 0:07:02
0:07:02
 0:10:38
0:10:38
 0:07:32
0:07:32
 0:11:20
0:11:20
 0:04:36
0:04:36
 0:05:11
0:05:11
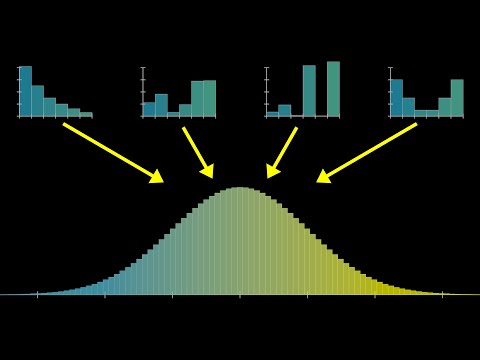 0:31:15
0:31:15
 0:05:14
0:05:14
 0:01:47
0:01:47
 0:23:16
0:23:16
 0:10:00
0:10:00
 0:01:16
0:01:16
 0:07:56
0:07:56
 0:13:37
0:13:37
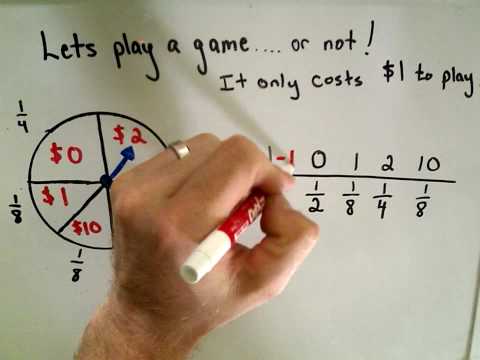 0:07:58
0:07:58