filmov
tv
Proof of A △ (B △ C) = (A △ B) △ C (Associativity of the Symmetric Difference)

Показать описание
In this exercise we will proof the associativity of the symmetric difference of three sets.
⏰ Timeline
00:00 Exercise
00:26 Symmetric difference
01:09 Simplifying
03:51 Symmetric difference of the right side
04:14 Simplifying
04:46 Comparing
05:15 Conclusion
🔢 Equation to proof
A △ (B △ C) = (A △ B) △ C
📜 All Discrete Mathematics Exercises
📜 All Linear Algebra Exercises
🎵 Music
Creative Commons — Attribution 3.0 Unported — CC BY 3.0
⏰ Timeline
00:00 Exercise
00:26 Symmetric difference
01:09 Simplifying
03:51 Symmetric difference of the right side
04:14 Simplifying
04:46 Comparing
05:15 Conclusion
🔢 Equation to proof
A △ (B △ C) = (A △ B) △ C
📜 All Discrete Mathematics Exercises
📜 All Linear Algebra Exercises
🎵 Music
Creative Commons — Attribution 3.0 Unported — CC BY 3.0
Proof of the tan(A+B)
Digital Electronics: Proof of a Boolean Identity (A+A'B=A+B)
Visual Proof for sin(A+B) = sinAcosB + cosAsinB
Number Theory Proof: If a|b and b|a then a = b or a = -b
Sine and Cosine Addition Formula Proof
Set Theory Proof (A\B) n B = Empty!
Proof of angle addition formula for sine | Trigonometry | Khan Academy
(a+b)3 formula proof
Trigonometry ||Trigonometry Day03||Trigonometry Prove that Questions ||Trigonometry Class 10
Proof of sin(A+B)=sinAcosB+cosAsinB
Proof: A'-B' = B-A (Double Inclusion) | Set Theory
Principle of Mathematical Induction (ab)^n = a^n*b^n Proof
Proof: Product of Absolute Values is the Absolute Value of the Product
Proof that 1 = 2.
Visual proof of sin(A+B) and cos(A+B) in one picture
How to do a PROOF in SET THEORY - Discrete Mathematics
Visual Proof: Squaring a Sum (a+b)²
tan(A+B)= (tanA + tanB)/(1 - tanAtanB) - Real Proof
Proof of cos(A+B) formula
a2 - b2 = (a+b) (a- b) but WHY Proof that a2 - b2 = (a+b) (a - b) !!! Math Mantra Video !!!
(A+B)^2 formula proof. | Tamil | LMES
Set Theory Proof A is a subset of B if and only if A intersect B = A
(a+b)^2 | a plus b whole square | Visual - Geometric Proof
a²-b²=(a+b)(a-b) Proof | A square minus b Square Identity Proof
Комментарии
 0:05:21
0:05:21
 0:01:18
0:01:18
 0:01:20
0:01:20
 0:07:04
0:07:04
 0:08:47
0:08:47
 0:01:59
0:01:59
 0:08:26
0:08:26
 0:03:28
0:03:28
 1:37:36
1:37:36
 0:04:18
0:04:18
 0:04:30
0:04:30
 0:03:52
0:03:52
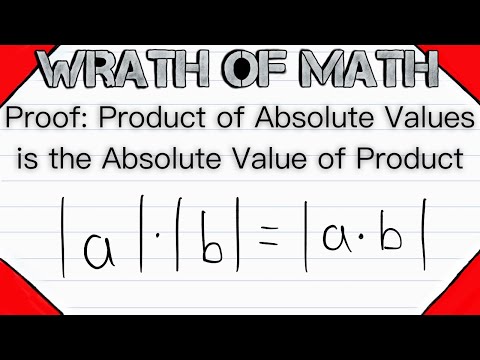 0:05:15
0:05:15
 0:02:59
0:02:59
 0:09:25
0:09:25
 0:16:30
0:16:30
 0:09:34
0:09:34
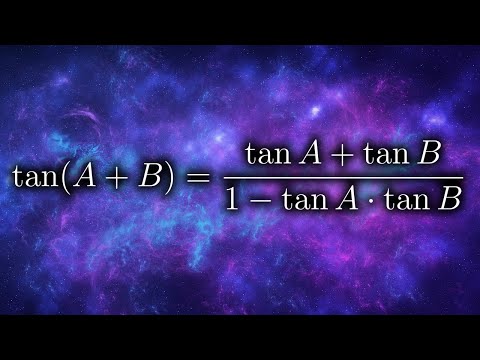 0:08:33
0:08:33
 0:13:49
0:13:49
 0:08:09
0:08:09
 0:04:01
0:04:01
 0:05:39
0:05:39
 0:01:38
0:01:38
 0:00:39
0:00:39