COSIC seminar 'MozZarella: Efficient Vector-OLE and...' (Lennart Braun, Aarhus University)

COSIC seminar – MozZarella: Efficient Vector-OLE and Zero-Knowledge Proofs Over $\Z_{2^k}$ – Lennart Braun (Aarhus University)

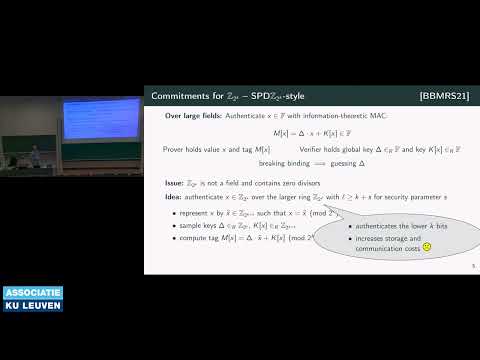
Zero-Knowledge Proof systems are usually designed to support computations for circuits over a field $\F_2$ or $\F_p$ for large $p$, but not for computations over rings $\Z_{2^k}$, which all modern CPUs operate on. Although $\Z_{2^k}$-arithmetic can be emulated using prime moduli, this comes with an unavoidable overhead. Recently, Baum et al. (CCS 2021) suggested a candidate construction for a Designated-Verifier Zero-Knowledge proof system that natively runs over $\Z_{2^k}$. Unfortunately, their construction requires preprocessed random vector oblivious linear evaluation (VOLE) to be instantiated over $\Z_{2^k}$. Currently, it is not known how to efficiently generate such random VOLE in large quantities.

In this work, we present a maliciously secure, VOLE extension protocol that can turn a short seed-VOLE over $\Z_{2^k}$ into a much longer, pseudorandom VOLE over the same ring. Our construction borrows ideas from recent protocols over finite fields, which we non-trivially adapt to work over $\Z_{2^k}$. Moreover, we show that the approach taken by the QuickSilver Zero-Knowledge proof system (Yang et al. CCS 2021) can be generalized to support computations over $\Z_{2^k}$. This new VOLE-based proof system, which we call QuarkSilver, yields better efficiency than the previous Zero-Knowledge protocols suggested by Baum et al. Furthermore, we implement both our VOLE extension and our Zero-Knowledge proof system, and show that they can generate 13–50 million VOLEs per second for 64 bit to 256 bit rings, and evaluate 1.3 million 64 bit multiplications per second in zero-knowledge.

This is joint work with Carsten Baum, Alexander Munch-Hansen and Peter Scholl from Aarhus University.