filmov
tv
probability density function of standard Cauchy variate and cauchy variate having two parameters

Показать описание
📚RECOMMENDED BOOKS :
►12th class math ncert books part 1&2 :
►12th class maths ncert solutions book :
HANDWRITTEN NOTES ON :
►Poisson distribution :
►negative binomial distribution :
►Geometric and Hypergeometric distribution :
👉OUR CHANNEL PLAYLISTS 👇
Don't forget to like 👍, share🔁 and subscribe💯✔️
►12th class math ncert books part 1&2 :
►12th class maths ncert solutions book :
HANDWRITTEN NOTES ON :
►Poisson distribution :
►negative binomial distribution :
►Geometric and Hypergeometric distribution :
👉OUR CHANNEL PLAYLISTS 👇
Don't forget to like 👍, share🔁 and subscribe💯✔️
Probability Density Functions
Probability Distribution Functions (PMF, PDF, CDF)
Probability Density Function of the Normal Distribution
What is a Probability Density Function (pdf)? ('by far the best and easy to understand explanat...
Find the Mean, Variance, and Standard Deviation Given the Probability Density Function
Probability Density Functions (1 of 7: Meeting the conditions)
Cumulative Distribution Functions and Probability Density Functions
Probability Density Function With Example | Probability And Statistics Tutorial | Simplilearn
STUDENT Maths Methods 2017 ATAR WACE Exam Attempt + Marking (97.4%)
Introduction to Probability Distributions
But what is the Central Limit Theorem?
Uniform Distribution EXPLAINED with Examples
Deriving the Mean and Variance of a Continuous Probability Distribution
Discrete Random Variables (3 of 3: Probability density function)
Continuous Probability Distributions - Basic Introduction
Normal distribution's probability density function derived in 5min
An Introduction to Continuous Probability Distributions
Probability of normal distribution
What is a Gaussian Distribution?
How normal probability distribution works
Probability Distribution Functions - PMF, PDF and CDF (Clearly Explained!)
Binomial distributions | Probabilities of probabilities, part 1
Probability Density Functions Examples || Lesson 63 || Probability & Statistics || Learning Monk...
Calculating probability using a probability density function
Комментарии
 0:11:46
0:11:46
 0:16:17
0:16:17
 0:13:32
0:13:32
 0:09:46
0:09:46
 0:09:38
0:09:38
 0:07:17
0:07:17
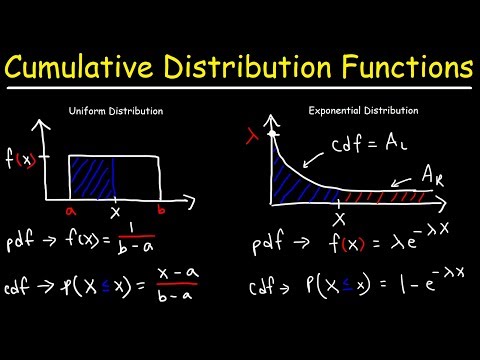 0:11:02
0:11:02
 0:25:26
0:25:26
 2:21:18
2:21:18
 0:06:20
0:06:20
 0:31:15
0:31:15
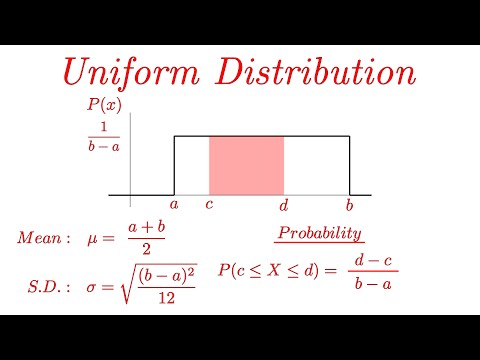 0:06:05
0:06:05
 0:07:22
0:07:22
 0:09:52
0:09:52
 0:10:13
0:10:13
 0:04:50
0:04:50
 0:05:52
0:05:52
 0:00:05
0:00:05
 0:05:45
0:05:45
 0:00:59
0:00:59
 0:16:20
0:16:20
 0:12:34
0:12:34
 0:05:51
0:05:51
 0:04:43
0:04:43