filmov
tv
Определение синуса, косинуса и тангенса углов

Показать описание
Тригонометрия. Определение синуса, косинуса и тангенса углов.
ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по Математике...
Синус, косинус, тангенс, котангенс за 5 МИНУТ
ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, Котангенс
Как видеть тангенс? Тангенс угла с помощью единичного круга....
Определение синуса, косинуса и тангенса угла
Опредение синуса, косинуса, тангенса, котангенса. Видеоурок 21. Алгебра 10 класс...
Синус, косинус произвольного угла. 9 класс.
Определение синуса, косинуса и тангенса в одном видео! #математикадлядетей #онлайнматематика...
СУТЬ ТРИГОНОМЕТРИИ
Определение синуса, косинуса и тангенса углов
Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэ...
За халявой переходи в шапку профиля #огэ #онлайншкола #математика #егэ...
Как запомнить значения синусов и косинусов?! #математика #синус #косинус #геометрия #егэ #shorts...
Что такое синус, косинус, тангенс и котангенс объяснение...
Таблица значений синуса, косинуса, тангенса и котангенса....
8 класс, 30 урок, Значения синуса, косинуса и тангенса для углов 30◦, 45◦ и 60◦...
Значения синуса и косинуса для разных углов. Онлайн школа EXAMhack...
Что такое синус, косинус, тангенс и котангенс
Значения синуса, косинуса и тангенса некоторых углов
ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА 30, 45 И 60 ГРАДУСОВ
Тригонометрическая окружность. Как выучить?
Урок 1. Определение синуса, косинуса, тангенса, котангенса острого угла прямоугольного треугольника...
Определение синуса, косинуса, тангенса, котангенса// Алгебра// 9 класс...
Значения синуса, косинуса, тангенса и котангенса некоторых углов...
Комментарии
 0:09:24
0:09:24
 0:05:25
0:05:25
 0:06:18
0:06:18
 0:04:30
0:04:30
 0:10:31
0:10:31
 0:06:53
0:06:53
 0:18:53
0:18:53
 0:00:24
0:00:24
 0:08:29
0:08:29
 0:22:12
0:22:12
 0:00:26
0:00:26
 0:00:59
0:00:59
 0:00:18
0:00:18
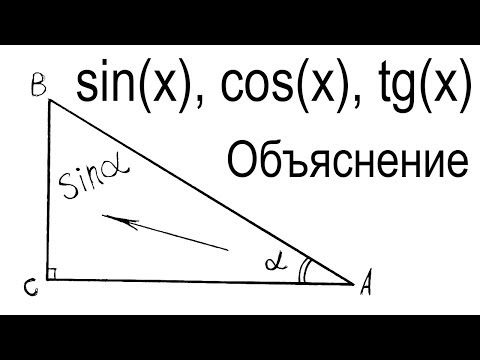 0:16:45
0:16:45
 0:31:31
0:31:31
 0:06:12
0:06:12
 0:00:18
0:00:18
 0:00:41
0:00:41
 0:04:47
0:04:47
 0:14:56
0:14:56
 0:10:22
0:10:22
 0:10:13
0:10:13
 0:10:59
0:10:59
 0:09:51
0:09:51