filmov
tv
Linear Maps - 5

Показать описание
We prove that if V and W are finite dimensional vector spaces, then the dimension of L(V,W) is the product of the dimensions of V and W.
We define linear isomorphism and give some examples. We point out the bijections used to construct vector space (in Esoteric Examples) are linear isomorphisms.
Finally, we prove that if V and W are finite dimensional vector spaces, then a linear map f from V to W is a linear isomorphism iff it is one-one and iff it is onto. Our proof does not use Rank-Nullity theorem, but in stead uses many basic results one has learned so far. So, this may be an instructive proof. Later we shall prove it using the rank-nullity theorem.
Timestamp provided by Ishwarya.
00:00 Introduction
0:52 Aim of the lecture
2:52 Theorem: dim (L(V, W))= product of dim(V) and dim(W)
24:53 Any 1-1 linear map maps linearly independent sets in V to linearly independent sets in W
29:01 Definition of linear isomorphism
31:32 Some examples
39:01 Digression to sets: If A,B are finite sets and both have same cardinality & if f is 1-1 then f is onto, vice-versa.
40:37 Summary of the observation
42:01 Theorem: f is linear isomorphism iff f is 1-1 & iff f is onto
We define linear isomorphism and give some examples. We point out the bijections used to construct vector space (in Esoteric Examples) are linear isomorphisms.
Finally, we prove that if V and W are finite dimensional vector spaces, then a linear map f from V to W is a linear isomorphism iff it is one-one and iff it is onto. Our proof does not use Rank-Nullity theorem, but in stead uses many basic results one has learned so far. So, this may be an instructive proof. Later we shall prove it using the rank-nullity theorem.
Timestamp provided by Ishwarya.
00:00 Introduction
0:52 Aim of the lecture
2:52 Theorem: dim (L(V, W))= product of dim(V) and dim(W)
24:53 Any 1-1 linear map maps linearly independent sets in V to linearly independent sets in W
29:01 Definition of linear isomorphism
31:32 Some examples
39:01 Digression to sets: If A,B are finite sets and both have same cardinality & if f is 1-1 then f is onto, vice-versa.
40:37 Summary of the observation
42:01 Theorem: f is linear isomorphism iff f is 1-1 & iff f is onto
 0:10:59
0:10:59
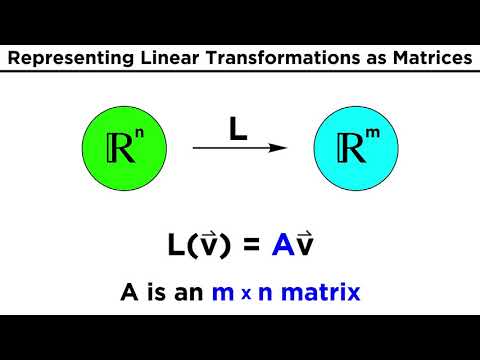 0:09:11
0:09:11
 0:54:25
0:54:25
 0:04:46
0:04:46
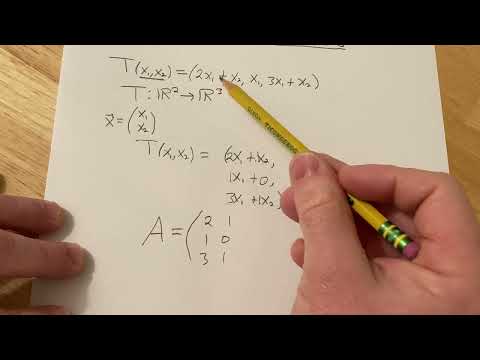 0:05:19
0:05:19
 0:13:52
0:13:52
 0:16:01
0:16:01
 0:06:58
0:06:58
 0:09:46
0:09:46
 0:06:46
0:06:46
 0:11:32
0:11:32
 1:12:04
1:12:04
 0:11:23
0:11:23
![[Linear Algebra] Linear](https://i.ytimg.com/vi/cFIRXQBfgg0/hqdefault.jpg) 0:12:30
0:12:30
 0:11:23
0:11:23
 0:07:49
0:07:49
 0:09:06
0:09:06
 0:18:02
0:18:02
 0:04:09
0:04:09
 0:08:25
0:08:25
 0:12:51
0:12:51
 0:12:21
0:12:21
 0:09:20
0:09:20
 0:01:34
0:01:34