Change of basis and Taylor coefficient vectors | Wild Linear Algebra A 26 | NJ Wildberger

In this lecture we put our previous discussion of coordinate vectors and change of basis into a more general and novel framework, and look at an important application to calculus.

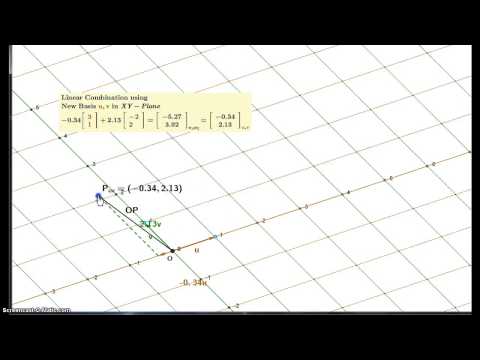
We introduce the new idea of a vatrix: a matrix whose entries are themselves vectors. This concept allows us to encode the basis of a linear/vector space, such as P^3, as a vector, and linear combinations as products of row and column vatrices. Coefficient vectors now become row vectors, and change of basis matrices have a logical and intuitive labelling.

Our main example goes right back to our first lecture with Bob and Rachel's two bases for the affine plane. Then we look at Taylor coefficient vectors for a polynomial p in P^3. For every rational point c there is a Taylor basis, with an associated vatrix of powers of (alpha-c). The crucial change of basis matrices are generalized Pascal matrices which enjoy lovely algebraic properties--they form a one-parameter group of matrices.

In fact this whole theory has natural connections with the representation theory of sl(2), which we do not mention. This is the final lecture in this first half of this course on Linear Algebra.

************************

Here are the Insights into Mathematics Playlists:

Here are the Wild Egg Maths Playlists (some available only to Members!)

************************

[njwildberger]

Thanks. It is one of my long term projects to look at this Grassman, Clifford Hestenes algebra carefully. I am aware of some of its advantages, and clearly a synthesis between it and rational trigonometry would be fruitful.

I may well try to make some lectures on that some day. Thanks for the suggestion.

[peterhi]

Your work here remains fantastic. A course on Geometric Algebra, based on the work of Hestenes, seems to be a very natural synthesis and continuation of the material you've presented in many of your courses. The topic is very much in the spirit of your work: it has a strong geometric flavor, it unifies many themes, and it vastly expands the scope of geometric manipulations that can be performed algebraically. The degree to which it simplifies many branches of physics is astonishing. Best.

[PaulBeykirch]

You are not only a great mathematician, but a really great teacher! Im studying linal now at uni and your approach has provided another angle. Linal is amazing, the most cool math ive studied thus far. Thanks for your passion and willingness to share your knowledge.

[njwildberger]

One possibility might be to consider a more generalized vatrix which is a matrix (rather than a vector) whose entries are themselves vectors/polynomials. Coefficients would be another matrix of numbers. We would then want to `multiply' these two to get the corresponding linear combination of polynomials. I haven't given any thought to how this would work..

[Chemistrryy]

You are just a really good teacher. Your lectures saved me a lot of time. Just one comment, I have never found your lectures before today. I really would have liked to find them earlier. The lectures would have been easier to find if you had written whole titles such as 'Linear Algebra' instead of or in addition to your abbrivation 'WildLinAlg'. Thanks for the lecture!

[pickeyberry]

Video Content

00:00 Introduction
06:26 There are two different kinds of linear relations: relation between vectors and relation between coefficients
10:56 Algebric operations with matrices
13:31 Definition. A vatrix is a matrix whose entries are all vectors (of the same size)
16:24 Co-ordinate vectors
19:39 Change of basis
23:36 Note. We are changing our notation here from previous lectures. Now co-ordinate vectors are row vectors
29:17 Taylor coefficient vectors

[Cor]

Thank very much for your work done so far!
The polynomial basis can be seen as a vector containing vectors (1, alpha, alpha^2, ..) Suppose we have a polynomial with 2 generators, alpha an beta.Then the basis would be some thing like (1, alpha, beta, alpha^2, alphabeta, beta^2, ...). With an order 5 polynomial one would already have 26 entries in this vatrix. How does your notation cope with increasing orders and number of polynomial generators? Is there some kind of Einstein notation possible?