Proof trees for different modal logics | Logic tutorial | Attic Philosophy

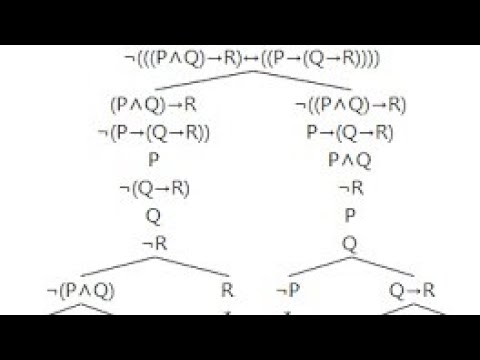
Proof trees are a great way to build proofs and test arguments in modal logic. They're also a helpful way to understand the possible world semantics for modal logic. In the previous video, I showed you how to use proof trees for the basic system of modal logic, K. In this video, I'll show you how to extend proof trees for other modal system: KT, KD, KB, K4 and K5, as well as combinations – systems like KD45. It's much simpler than it sounds!

Correction: at 2:20, the rule written on the right should read:

¬♢A, n
|
☐¬A, n

Here's some general background on Proof Trees:

00:00 - Intro
01:01 - Recap: modal trees
01:35 - Recap: rules for modalities
02:30 - How to construct a proof
02:47 - Other modal systems
03:22 - 5 new systems: D, T, B, 4, 5
04:33 - The D rule
05:04 - The T rule
05:28 - The B rule
05:51 - The 4 rule
06:15 - The 5 rule
06:40 - Combining modal systems
07:44 - Wrap up

If there’s a topic you’d like to see covered, leave me a comment below.

Links:

Get in touch on Social media!

#logic #modality #proofs

[AtticPhilosophy]

How are you getting on with modal proof trees? Any problems so far? Leave me a question below!

[jeetghosh]

It's very helpful to me and others also..

[demitriemanuel]

I’m using Donald Kalish’s book, Logic: Techniques of Formal Reasoning. The problem is that it doesn’t have enough logic problems to work with, nor does it contain the answers to many of the problems. What would you recommend to someone for self study? I want to get a good grasp on logic but I can’t seem to find a good source with more things to solve. Any recommendations? Thank you

[khoiangnguyen]

Uhm, in 2:20, shouldn't it be ~<>A, n -> []~A, n (You wrote ~[]A instead)? If A is not possible in any accessible world (~<>A), then there would be no accessible world that A is true, which means A is false in every accessible world, implying not A is a necessity for all possible world ([]~A).