filmov
tv
An Insane Approach! The Fresnel integrals: sin(x^2) and cos(x^2) without complex analysis

Показать описание
Help me create more free content! =)
Visit my website! =)
In today's video we are going to play around with the integral of e^(-ix^2) from -infinity to infinity. With this one integral we are going to be able to evaluate the two Fresnel integrals. But not in the complex way! Let's solve it by using algebraic methods and differentiation under the integral sign, also known as the Leibniz rule for integrals or Feynman integration. Have fun =)
The Fresnel integrals without complex analysis: an insane approach better than @PapaFlammy69 lol😂
An Insane Approach! The Fresnel integrals: sin(x^2) and cos(x^2) without complex analysis
The coolest way to evaluate the Fresnel integrals (Feynman's technique)
A beautiful approach to the Fresnel integrals using complex analysis
A fascinating approach to the Fresnel integrals
Fresnel integrals: how 2 math ft. DJ limit ( Still needs an update of some sort )
Using a Maclaurin Series to Compute the Fresnel Sine Integral, Superquiz 3 Problem 8
🔴MATHSCLIC SHORTS | INTÉGRALES DE FRESNEL
Feynman’s Technique is Unstoppable!!! | Fresnel Integrals
Ramanujan's master theorem is insanely overpowered!!! example using the Fresnel integrals
See What REALLY Goes Into a Carrier Landing
Do hot objects fall through water faster? Leidenfrost Effect!
A generalized Fresnel integral: int from zero to infinity of sin(x^n)
A crazy approach to the gaussian integral using Feynman's technique
The Generalized Fresnel Integrals
How US Navy Pilots Pull Off Scary Landings on Crowded Aircraft Carrier at Sea
Asking Laplace to help us solve the Fresnel integral without complex analysis
This Result looks WAY TOO GOOD to be True! Transforming transcendental bois!
intro samarox
The Fresnel Integrals! (A Few LIGHT Integrals)
Evaluate the limit as x approaches 1 for (integral cos t dt)/(x^2 -1) over (1, x]. l’Hopital’s Rule...
03. Diffraction Integrals (Fresnel + Fraunhofer propagation, Point Spread Function, Fourier optics)
Integrating one outdated Boi | MIT Integration Bee 2015 ( Papa Flammy's Integral Week )
How FLOLS Works
Комментарии
 0:15:50
0:15:50
 0:21:07
0:21:07
 0:21:41
0:21:41
 0:06:59
0:06:59
 0:14:01
0:14:01
 0:02:48
0:02:48
 0:04:44
0:04:44
 0:00:34
0:00:34
 0:18:02
0:18:02
 0:11:07
0:11:07
 0:11:27
0:11:27
 0:04:44
0:04:44
 0:15:12
0:15:12
 0:11:04
0:11:04
 0:17:49
0:17:49
 0:15:49
0:15:49
 0:07:27
0:07:27
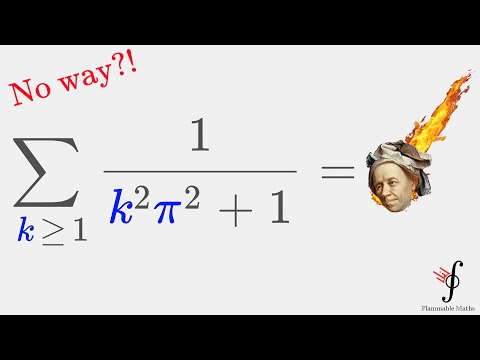 0:10:33
0:10:33
 0:00:11
0:00:11
 0:11:58
0:11:58
 0:02:01
0:02:01
 0:25:59
0:25:59
 0:03:19
0:03:19
 0:07:53
0:07:53