filmov
tv
The economic production quantity: solved problem_3

Показать описание
Effective inventory management is essential for most businesses' successful operations and supply chains. This is because inventory management impacts operations, marketing, and finance. Poor inventory management hampers operations diminish customer satisfaction, and increases operating costs.
Here we will learn the inventory ordering policies.
Inventory ordering policies address the two basic issues of inventory management, which are how much to order and when to order.
Several models are described that are used for these issues.
Inventory that is intended to meet expected demand is known as cycle stock, while inventory that is held to reduce the probability of experiencing a stock out (i.e., running out of stock) due to demand and/or lead time variability is known as safety stock.
The discussion begins with the issue of how much to order.
The question of how much to order can be determined by using an economic order quantity (or EOQ) model. E O Q models identify the optimal order quantity by minimizing the sum of certain annual costs that vary with order size and order frequency. Three order size models are described here:
The basic economic order quantity model.
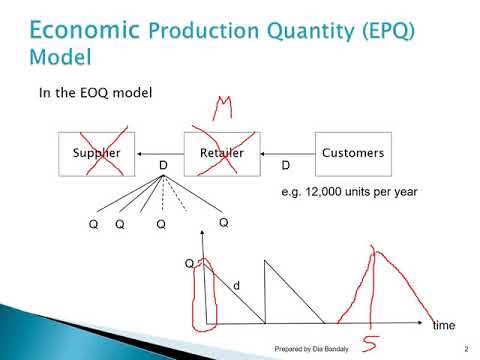
The economic production quantity model.
The quantity discount model.
The economic production quantity model (EPQ model) is explained in this video by solving a problem.
Knowing how much to order or the production lot size is an essential issue in production planning.
You can obtain this piece of information using the economic production quantity model. This model is widely used in production. Even in assembly operations, portions of the work are done in batches.
This model is extensively explained in another video, to watch that video click the above link.
Here a problem will be solved to show you how to apply this model in reality.
This is problem number 11 in the Operations Management Book by William Stevenson.
A company is about to begin production of a new product. The manager of the department that will produce one of the components for the new product wants to know how often the machine used to produce the item will be available for other work. The machine will produce the item at a rate of 200 units daily. Eighty units will be used daily in assembling the final product. Assembly will take place five days a week, 50 weeks a year. The manager estimates that it will take almost a full day to get the machine ready for a production run, for $300. Inventory holding costs will be $10 a year.
Solve the following questions:
What run quantity should be used to minimize total annual costs?
How many days does it take to produce the optimal run quantity?
What is the average amount of inventory?
If the manager wants to run another job between runs of this item and needs a minimum of 10 days per cycle for the other work, will there be enough time?
Given your answer to the previous question, 4, the manager wants to explore options that will allow this other job to be performed using this equipment. Name three options the manager can consider.
Suppose the manager decides to increase the run size of the new product. How many additional units would be needed to just accommodate the other job? How much will that increase the total annual cost?
Here we will learn the inventory ordering policies.
Inventory ordering policies address the two basic issues of inventory management, which are how much to order and when to order.
Several models are described that are used for these issues.
Inventory that is intended to meet expected demand is known as cycle stock, while inventory that is held to reduce the probability of experiencing a stock out (i.e., running out of stock) due to demand and/or lead time variability is known as safety stock.
The discussion begins with the issue of how much to order.
The question of how much to order can be determined by using an economic order quantity (or EOQ) model. E O Q models identify the optimal order quantity by minimizing the sum of certain annual costs that vary with order size and order frequency. Three order size models are described here:
The basic economic order quantity model.
The economic production quantity model.
The quantity discount model.
The economic production quantity model (EPQ model) is explained in this video by solving a problem.
Knowing how much to order or the production lot size is an essential issue in production planning.
You can obtain this piece of information using the economic production quantity model. This model is widely used in production. Even in assembly operations, portions of the work are done in batches.
This model is extensively explained in another video, to watch that video click the above link.
Here a problem will be solved to show you how to apply this model in reality.
This is problem number 11 in the Operations Management Book by William Stevenson.
A company is about to begin production of a new product. The manager of the department that will produce one of the components for the new product wants to know how often the machine used to produce the item will be available for other work. The machine will produce the item at a rate of 200 units daily. Eighty units will be used daily in assembling the final product. Assembly will take place five days a week, 50 weeks a year. The manager estimates that it will take almost a full day to get the machine ready for a production run, for $300. Inventory holding costs will be $10 a year.
Solve the following questions:
What run quantity should be used to minimize total annual costs?
How many days does it take to produce the optimal run quantity?
What is the average amount of inventory?
If the manager wants to run another job between runs of this item and needs a minimum of 10 days per cycle for the other work, will there be enough time?
Given your answer to the previous question, 4, the manager wants to explore options that will allow this other job to be performed using this equipment. Name three options the manager can consider.
Suppose the manager decides to increase the run size of the new product. How many additional units would be needed to just accommodate the other job? How much will that increase the total annual cost?
 0:08:03
0:08:03
 0:04:21
0:04:21
 0:10:47
0:10:47
 0:08:53
0:08:53
 0:11:35
0:11:35
 0:14:59
0:14:59
 0:02:05
0:02:05
 0:12:20
0:12:20
 0:05:25
0:05:25
 0:02:41
0:02:41
 0:06:54
0:06:54
 0:06:22
0:06:22
 0:07:29
0:07:29
 0:03:33
0:03:33
 0:07:41
0:07:41
 0:32:49
0:32:49
 0:23:13
0:23:13
 0:14:19
0:14:19
 0:06:37
0:06:37
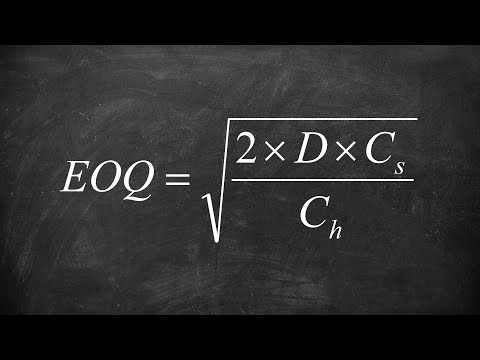 0:05:15
0:05:15
 0:12:37
0:12:37
 0:05:16
0:05:16
 0:12:06
0:12:06
 0:03:14
0:03:14